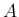 が
が 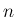 次正方行列、
次正方行列、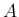 による
による 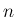 次元数ベクトル
次元数ベクトル
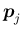 (
(
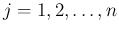 ) の像が
) の像が
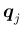 、すなわち
、すなわち
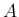 が
が 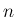 次正方行列、
次正方行列、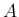 による
による 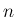 次元数ベクトル
次元数ベクトル
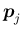 (
(
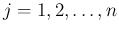 ) の像が
) の像が
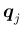 、すなわち
、すなわち
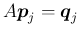
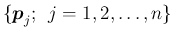 が一次独立であるとき、
が一次独立であるとき、
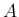 を
を
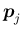 ,
,
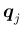 で表してみよう。
で表してみよう。
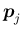 ,
,
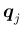 を並べてできる
を並べてできる 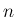 次正方行列を
それぞれ
次正方行列を
それぞれ 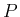 ,
, 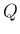 とする:
とする:
![$\displaystyle P=[\mbox{\boldmath$p$}_1\ \mbox{\boldmath$p$}_2\ \cdots\ \mbox{\b...
...=[\mbox{\boldmath$q$}_1\ \mbox{\boldmath$q$}_2\ \cdots\ \mbox{\boldmath$q$}_n]
$](img68.png)
![$\displaystyle AP
= A[\mbox{\boldmath$p$}_1\ \mbox{\boldmath$p$}_2\ \cdots\ \mb...
...box{\boldmath$q$}_1\ \mbox{\boldmath$q$}_2\ \cdots\ \mbox{\boldmath$q$}_n]
= Q
$](img69.png)
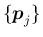 が一次独立なので
が一次独立なので 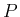 は正則、
すなわち逆行列を持つので、よって、
は正則、
すなわち逆行列を持つので、よって、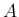 は
は 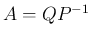 と書ける。
このようにして、
と書ける。
このようにして、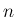 次元の一次変換行列
次元の一次変換行列 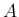 は、
は、
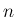 個の一次独立なベクトルとその像によって決定することができる。
個の一次独立なベクトルとその像によって決定することができる。
竹野茂治@新潟工科大学