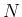
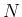 次元数ベクトルは、
とし、そしてこの元を、
次元数ベクトルは、
とし、そしてこの元を、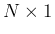 行列
行列
![$\displaystyle \mbox{\boldmath$a$}=\left[\begin{array}{c}{a_1}\\ {a_2}\\ \vdots\\ {a_N}
\end{array}\right]
$](img14.png)
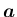 のように
小文字の太字で表す。
のように
小文字の太字で表す。
それに対して、行ベクトル、
すなわち 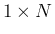 行列
行列
![$A=[a_1\ a_2\ \cdots\ a_N]$](img17.png) は
それとは異なるものとし、あくまで行列であると考え、
転置によって通常のベクトルになると考える。すなわち、
は
それとは異なるものとし、あくまで行列であると考え、
転置によって通常のベクトルになると考える。すなわち、
![$\displaystyle \,{}^T\!{A}=\left[\begin{array}{c}{a_1}\\ {a_2}\\ \vdots\\ {a_N}
\end{array}\right]=\mbox{\boldmath$a$}
$](img18.png)
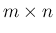 行列
行列
![$A=[a_{ij}]_{m,n}$](img2.png) は、
各列の列ベクトル (
は、
各列の列ベクトル (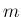 次元)
次元)
![$\displaystyle \mbox{\boldmath$a$}_j = \left[\begin{array}{c}{a_{1j}}\\ {a_{2j}}\\ \vdots\\ {a_{mj}}
\end{array}\right]
$](img20.png)
![$A = [\mbox{\boldmath$a$}_1\ \mbox{\boldmath$a$}_2\ \cdots \mbox{\boldmath$a$}_n]$](img21.png) と表され、
また、各行の行ベクトル
と表され、
また、各行の行ベクトル
![$A_i=[a_{i1}\ a_{i2}\ \cdots a_{in}]$](img22.png) の転置の
ベクトル (
の転置の
ベクトル (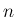 次元)
次元)
![$\displaystyle \,{}^T\!{A}_i = \mbox{\boldmath$\hat{a}$}_i = \left[\begin{array}{c}{a_{i1}}\\ {a_{i2}}\\ \vdots\\ {a_{in}}
\end{array}\right]
$](img24.png)
![$\displaystyle A = \left[\begin{array}{c}{A_1}\\ {A_2}\\ \vdots\\ {A_m}
\end{ar...
...}$}_2}}\\ \vdots\\ {\,{}^T\!{\mbox{\boldmath$\hat{a}$}_m}}
\end{array}\right]
$](img25.png)
なお、すでに何度か使っているが、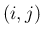 成分が
成分が 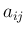 であるような
であるような
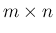 行列のことを、本稿では
行列のことを、本稿では
![$[a_{ij}]_{m,n}$](img28.png) と書くことにする。
と書くことにする。
竹野茂治@新潟工科大学