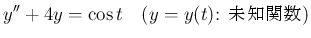 (16)
(16)
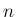 階
微分方程式
の形に帰着させることもできる。
階
微分方程式
の形に帰着させることもできる。
例えば、(16) は、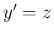 (
(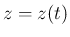 : 未知) とすれば、
: 未知) とすれば、
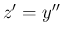 より
より
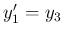 ,
, 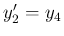 と
すれば
の 1 階連立となる。
逆に、(17) から
と
すれば
の 1 階連立となる。
逆に、(17) から 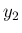 (または
(または 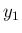 ) を
消去して
) を
消去して 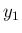 の 4 階微分方程式を作ることもできる。
それには、演算子法を利用すると便利だが、その詳しい説明は
微分方程式の本を参照してもらうことにして、
その計算だけを紹介する。
(17) は微分演算子
の 4 階微分方程式を作ることもできる。
それには、演算子法を利用すると便利だが、その詳しい説明は
微分方程式の本を参照してもらうことにして、
その計算だけを紹介する。
(17) は微分演算子 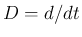 を用いて
を用いて
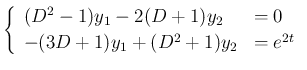
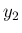 を消去すれば、
を消去すれば、
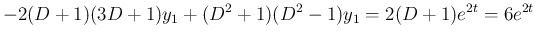
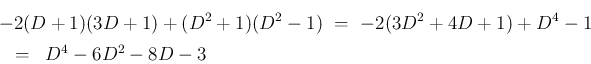
よって、1 階連立方程式 (18) を
解くことと 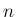 階単独方程式 (19) を解くことは
実質的に同じで、
微分方程式の本では通常どちらかの解法のみを紹介し、
他方の方程式はそちらに変換する方法を紹介する、というのが普通である。
階単独方程式 (19) を解くことは
実質的に同じで、
微分方程式の本では通常どちらかの解法のみを紹介し、
他方の方程式はそちらに変換する方法を紹介する、というのが普通である。
一般的には、より解法を重視する工学系の教科書では
単独方程式 (19) の方で解法を紹介し、
理論を重視する理学系の教科書では
連立方程式 (18) の方で解法を紹介することが
多いように思う。
それは、連立方程式 (18) の解法には行列の理論、
特に 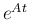 の話が必要になるからだと思われる。
単独方程式 (19) の場合は、
行列を使用せずに特性方程式 (連立方程式 (18) の
場合の固有方程式に対応する) を解くことで、代入法や定数変化法、演算子法、
ラプラス変換などにより行列を用いずに解を求めることができる。
の話が必要になるからだと思われる。
単独方程式 (19) の場合は、
行列を使用せずに特性方程式 (連立方程式 (18) の
場合の固有方程式に対応する) を解くことで、代入法や定数変化法、演算子法、
ラプラス変換などにより行列を用いずに解を求めることができる。
なお、(18) や (19) の
係数 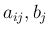 が定数でない場合、すなわち
が定数でない場合、すなわち 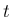 の既知関数である場合は、
方程式の解法は特殊な場合にしか存在せず、問題はかなり難しい。
本節では定数係数の場合のみ扱う。
の既知関数である場合は、
方程式の解法は特殊な場合にしか存在せず、問題はかなり難しい。
本節では定数係数の場合のみ扱う。
方程式に現れる既知関数 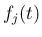 がすべて 0 である場合の方程式を斉次形、
一つでも 0 でないものがある場合は非斉次形と呼ぶ。
がすべて 0 である場合の方程式を斉次形、
一つでも 0 でないものがある場合は非斉次形と呼ぶ。
![$\displaystyle Y(t) = \left[\begin{array}{c}{y_1(t)}\\ {y_2(t)}\\ \vdots\\ {y_n(...
...{f_2(t)}\\ \vdots\\ {f_n(t)}
\end{array}\right],
\hspace{1zw}A=[a_{ij}]_{i,j}
$](img261.png)
![$\displaystyle Y(t_0)=Y_0=\left[\begin{array}{c}{\alpha_1}\\ {\alpha_2}\\ \vdots\\ {\alpha_n}
\end{array}\right]
$](img263.png)
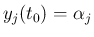 ) を満たす解を考える。
) を満たす解を考える。
 の斉次方程式の場合、
の斉次方程式の場合、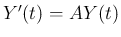 の初期値問題の解は、
一意的に
の初期値問題の解は、
一意的に
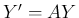 の両辺に
の両辺に 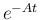 を左からかけると、
定理 5.3 により、
を左からかけると、
定理 5.3 により、
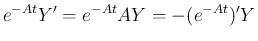
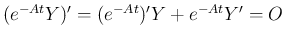 となるので
となるので 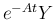 は
定数行列であることになる。よって
は
定数行列であることになる。よって
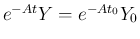 となるので、
両辺に
となるので、
両辺に 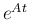 をかければ (24) が得られる。
をかければ (24) が得られる。
より一般の非斉次方程式の場合は、
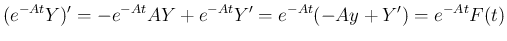
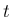 に関して
に関して 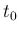 から
から 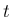 まで両辺を積分すると
まで両辺を積分すると
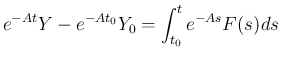
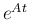 倍して移項すれば、
が得られる。
いずれも、
倍して移項すれば、
が得られる。
いずれも、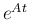 の計算によって解がシンプルな形で表現されることになる。
の計算によって解がシンプルな形で表現されることになる。
さて、これらを用いて、実際に (20) の 初期値問題
および (21) の初期値問題 の解を求めてみる。(20) は、
![$\displaystyle \left[\begin{array}{c}y\\ z\end{array}\right]'
= \left[\begin{ar...
...\cos t\end{array}\right]
= A\left[\begin{array}{c}y\\ z\end{array}\right]+F(t)
$](img279.png)
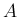 の固有値は、
の固有値は、
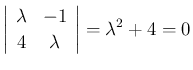
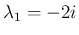 ,
, 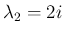 、固有ベクトルは
、固有ベクトルは
![$\displaystyle \mbox{\boldmath$x$}_1=\left[\begin{array}{c}1\\ \lambda_1\end{arr...
...1\\ \lambda_2\end{array}\right]=\left[\begin{array}{c}1\\ 2i\end{array}\right]
$](img284.png)
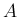 は対角化可能で、
は対角化可能で、
![$\displaystyle Q=[\mbox{\boldmath$x$}_1\ \mbox{\boldmath$x$}_2] = \left[\begin{a...
...ay}\right]
=\frac{1}{4}\left[\begin{array}{cc}2 & i\\ 2 & -i\end{array}\right]
$](img285.png)
![$\displaystyle Q^{-1}AQ
= \left[\begin{array}{cc}\lambda_1&0\\ 0&\lambda_2\end{...
...Q^{-1}e^{At}Q =\left[\begin{array}{cc}e^{-2it}&0\\ 0&e^{2it}\end{array}\right]
$](img286.png)
![$\displaystyle e^{At}\left[\begin{array}{c}y_0\\ z_0\end{array}\right]
=
\left...
...array}{c}y_0\cos 2t+(z_0/2)\sin 2t\\ -2y_0\sin 2t+z_0\cos 2t\end{array}\right]
$](img292.png)
![\begin{eqnarray*}\lefteqn{\int_0^te^{A(t-s)}\left[\begin{array}{c}0\\ \cos s\end...
...n{array}{c}\cos 3t+3\cos t-4\\ 2\sin 3t+6\sin t\end{array}\right]\end{eqnarray*}](img293.png)
![${}^T\!{[\alpha\ \beta]}/12$](img294.png) とし、
とし、
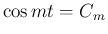 ,
, 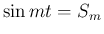 と略して書くと、
と略して書くと、
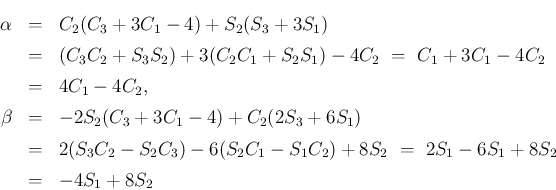
![$\displaystyle \int_0^te^{A(t-s)}\left[\begin{array}{c}0\\ \cos s\end{array}\rig...
...1}{3}\left[\begin{array}{c}\cos t-\cos 2t\\ -\sin t+2\sin 2t\end{array}\right]
$](img298.png)
![$\displaystyle \left[\begin{array}{c}y\\ z\end{array}\right]
=\left[\begin{array...
...1}{3}\left[\begin{array}{c}\cos t-\cos 2t\\ -\sin t+2\sin 2t\end{array}\right]
$](img299.png)
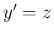 となること、
となること、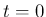 のとき
のとき
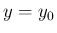 ,
, 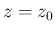 となることが容易に確認できる。
しかし、ここまでの手順はかなり長く、(16) を
単独方程式のまま特性方程式と代入法などで解く方がはるかに
短く容易である。
となることが容易に確認できる。
しかし、ここまでの手順はかなり長く、(16) を
単独方程式のまま特性方程式と代入法などで解く方がはるかに
短く容易である。
次は、(21) を考える。 こちらは最後までは計算しないが、 ジョルダン標準形位までは求めてみる。 この場合は、
![$\displaystyle Y=\left[\begin{array}{c}y_1\\ y_2\\ y_3\\ y_4\end{array}\right],
...
...],
\hspace{1zw}
F = \left[\begin{array}{c}0\\ 0\\ 0\\ e^{2t}\end{array}\right]
$](img303.png)
 の固有値から。
の固有値から。
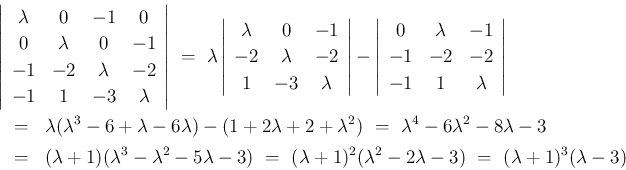
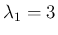 、
、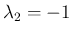 (重複度 3) となる。
(重複度 3) となる。
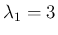 の固有空間は 1 次元で、固有ベクトル 1 つを求めればよい。
固有ベクトルの方程式は、
の固有空間は 1 次元で、固有ベクトル 1 つを求めればよい。
固有ベクトルの方程式は、
![$\displaystyle (A-3E)\mbox{\boldmath$x$}
=\left[\begin{array}{cccc}-3&0&1&0\\ 0&...
...t[\begin{array}{c}x_1\\ x_2\\ x_3\\ x_4\end{array}\right]
=\mbox{\boldmath$0$}
$](img307.png)
![\begin{eqnarray*}\lefteqn{A-3E
\ =\
\left[\begin{array}{cccc}-3&0&1&0\\ 0&-3...
...}{cccc}0&0&0&0\\ -1&1&0&0\\ -3&0&1&0\\ -3&0&0&1\end{array}\right]\end{eqnarray*}](img308.png)
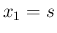 とすれば
とすれば 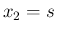 ,
, 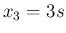 ,
, 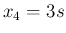 より
固有ベクトル
より
固有ベクトル
![$\displaystyle \mbox{\boldmath$v$}_1=\left[\begin{array}{c}1\\ 1\\ 3\\ 3\end{array}\right]s
$](img313.png)
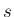 は
は 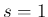 と取ればよい。
と取ればよい。
次は 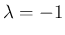 の固有ベクトルを考える。この場合は、
固有空間の次元は 3 以下だが、
の固有ベクトルを考える。この場合は、
固有空間の次元は 3 以下だが、
![\begin{eqnarray*}\lefteqn{A+E
\ =\
\left[\begin{array}{cccc}1&0&1&0\\ 0&1&0&...
...ay}{cccc}0&0&0&0\\ 1&1&0&0\\ 1&0&1&0\\ -1&0&0&1\end{array}\right]\end{eqnarray*}](img316.png)
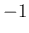 に対する固有ベクトルは、
に対する固有ベクトルは、
![$\displaystyle \mbox{\boldmath$v$}_2=\left[\begin{array}{c}1\\ -1\\ -1\\ 1\end{array}\right]s
$](img318.png)
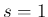 とすればよい。
固有値
とすればよい。
固有値 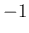 の重複度は 3 なので、この場合、
の重複度は 3 なので、この場合、
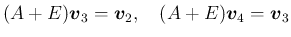
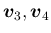 を取る必要がある。
なお、当然これらも一意に決定するわけではなく、例えば
を取る必要がある。
なお、当然これらも一意に決定するわけではなく、例えば
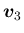 は、
は、
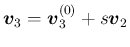
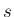 の自由度を持つ解が求まり、
の自由度を持つ解が求まり、
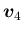 はその
はその 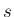 に対してさらに
に対してさらに
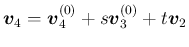
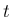 の自由度を持つ解が求まるはずである。
これらもとりあえずは
の自由度を持つ解が求まるはずである。
これらもとりあえずは  のように適当に固定してよい。
のように適当に固定してよい。
まずは
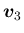 を求める。
方程式
を求める。
方程式
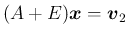 の解を求めるには、
拡大係数行列
の解を求めるには、
拡大係数行列
![$[A+E\ \mbox{\boldmath$v$}_2]$](img327.png) の
消去法を行う。実際には
の
消去法を行う。実際には 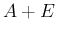 の部分の変形なので、その手順は
の部分の変形なので、その手順は
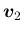 の
計算と同じで、違うのは一番右側の列のみとなる。
の
計算と同じで、違うのは一番右側の列のみとなる。
![\begin{eqnarray*}\lefteqn{[A+E\ \vert\ \mbox{\boldmath$v$}_2]
\ =\
\left[\beg...
...0&0&0\\ 1&1&0&0&1/2\\ 1&0&1&0&1\\ -1&0&0&1&-3/2\end{array}\right]\end{eqnarray*}](img330.png)
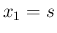 に対して
に対して 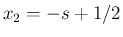 ,
, 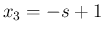 ,
, 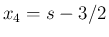 となり、
となり、
![$\displaystyle \mbox{\boldmath$v$}_3=s\left[\begin{array}{c}1\\ -1\\ -1\\ 1\end{array}\right]+\frac{1}{2}\left[\begin{array}{c}0\\ 1\\ 2\\ -3\end{array}\right]
$](img334.png)
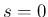 としたものを
としたものを
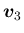 とする。
最後は
とする。
最後は
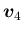 を求める。分数を消すために、方程式を 2 倍して、
を求める。分数を消すために、方程式を 2 倍して、
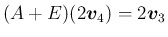
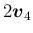 を求める計算を行う。
を求める計算を行う。
![\begin{eqnarray*}\lefteqn{[A+E\ \vert\ 2\mbox{\boldmath$v$}_3]
\ =\
\left[\be...
...0&0&0&0&0\\ 1&1&0&0&2\\ 1&0&1&0&0\\ -1&0&0&1&-1\end{array}\right]\end{eqnarray*}](img338.png)
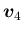 は
は
![$\displaystyle \mbox{\boldmath$v$}_4
=\frac{t}{2}\left[\begin{array}{c}1\\ -1\\ ...
...ray}\right]
+\frac{1}{2}\left[\begin{array}{c}0\\ 2\\ 0\\ -1\end{array}\right]
$](img339.png)
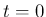 とすれば
とすれば
![$Q=[\mbox{\boldmath$v$}_1\ \mbox{\boldmath$v$}_2\ \mbox{\boldmath$v$}_3\ \mbox{\boldmath$v$}_4]$](img340.png) は
は
![$\displaystyle Q
=\left[\begin{array}{cccc}1&1&0&0\\ 1&-1&1/2&1\\ 3&-1&1&0\\ 3&1&-3/2&-1/2\end{array}\right]
$](img341.png)
![$\displaystyle J
=\left[\begin{array}{cc}J(3,1)&\raisebox{-.5ex}{\Large$0$}\\ [....
...[\begin{array}{cccc}3&0&0&0\\ 0&-1&1&0\\ 0&0&-1&1\\ 0&0&0&-1\end{array}\right]
$](img342.png)
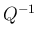 を求める。これも消去法で計算するが、
を求める。これも消去法で計算するが、
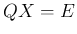 (
(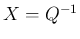 ) の両辺を 2 倍して、
) の両辺を 2 倍して、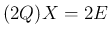 に対する拡大係数行列の
消去法を行い、なるべく分数計算を避けて計算する。
に対する拡大係数行列の
消去法を行い、なるべく分数計算を避けて計算する。
![\begin{eqnarray*}\lefteqn{[Q\ \vert\ 2E]
=
\left[\begin{array}{cccc\vert cccc...
...5&-4\\
0&0&8&0 &5&-2&3&-4\\ 0&0&0&2 &1&2&-1&0\end{array}\right]\end{eqnarray*}](img346.png)
![$\displaystyle Q^{-1}=\frac{1}{32}
\left[\begin{array}{cccc}3&2&5&4\\ 29&-2&-5&-...
... 29/32&-1/16&-5/32&-1/8\\
5/8&-1/4&3/8&-1/2\\ 1/2&1&-1/2&0\end{array}\right]
$](img347.png)
![\begin{eqnarray*}e^{J(3,1)t}
&=&
e^{3t},
\\
e^{J(-1,3)t}
&=&
e^{-t}\left...
...eft[\begin{array}{ccc}1&t&t^2/2\\ 0&1&t\\ 0&0&1\end{array}\right]\end{eqnarray*}](img348.png)
![$\displaystyle e^{Jt}
=\left[\begin{array}{cc}e^{J(3,1)t}&\raisebox{-.5ex}{\Larg...
...t}&te^{-t}&t^2e^{-t}/2\\
0&0&e^{-t}&te^{-t}\\ 0&0&0&e^{-t}\end{array}\right]
$](img349.png)
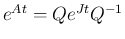 で
で 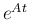 が求まり、
(25) を使えば
が求まり、
(25) を使えば 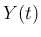 が求まる、
ということになる。
しかし、この先もかなり大変な計算が待っていることが想像できる。
が求まる、
ということになる。
しかし、この先もかなり大変な計算が待っていることが想像できる。
公式 (24), (25) は
一見シンプルな形であり、理論展開には便利で重要だが、
具体的な計算に向くかといえばそうでもなく、
特に大きな 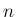 ではあまり実用的ではないことが
これらの例からもわかる。
ではあまり実用的ではないことが
これらの例からもわかる。
具体的な計算目的なら、むしろ単独方程式の方を特性方程式と代入法や 定数変化法 (やラプラス変換) などで解く方が易しい場合が多いだろう。
竹野茂治@新潟工科大学