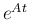
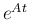 の積分について紹介する。
簡単なものは既に計算しているが、本稿ではより一般の
の積分について紹介する。
簡単なものは既に計算しているが、本稿ではより一般の 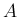 について考える。
について考える。
通常の関数からの類推で、
となることが容易に予想されると思う。実際、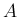 が正則であれば、
が正則であれば、
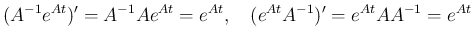
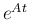 は
は 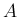 が正則ではない場合も存在し、
そして積分もできるので、その場合どうなるかも考えてみる。
が正則ではない場合も存在し、
そして積分もできるので、その場合どうなるかも考えてみる。
ジョルダン標準形による表現 (15) より、
![$\displaystyle \int e^{At}dt = Q\int e^{Jt}dt Q^{-1}
=Q\left[\begin{array}{ccc}\...
...isebox{0ex}{\LARGE$0$}} & \int e^{J(\lambda_s,k_s)t}dt\end{array}\right]Q^{-1}
$](img447.png)
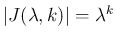 なので、
ジョルダン細胞
なので、
ジョルダン細胞 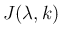 が正則であることは
が正則であることは 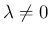 と
同値であり、その場合は
と
同値であり、その場合は
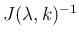 が存在し、
(38) により
が存在し、
(38) により
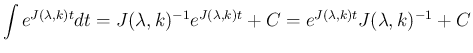
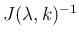 をここで求めておく。
をここで求めておく。
証明
(39) の右辺を 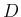 とすると、
とすると、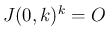 より、
より、
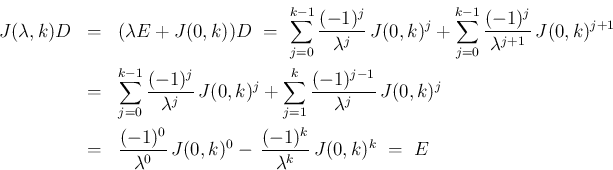
よって、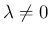 のときは、
のときは、
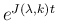 の積分は、
の積分は、
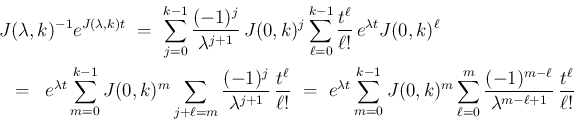
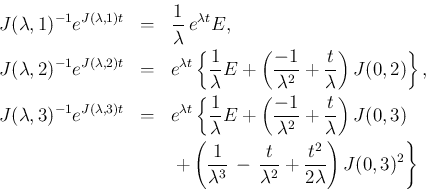
一方 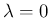 の場合は、
の場合は、
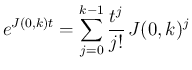
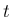 の多項式になるのでむしろ積分は容易で、
の多項式になるのでむしろ積分は容易で、
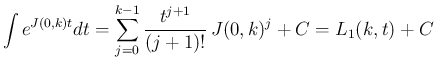
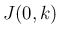 の逆行列では表現できないが、
これをあえて
の逆行列では表現できないが、
これをあえて  の場合の形に近い、
の場合の形に近い、
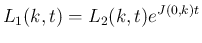
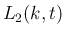 は
は
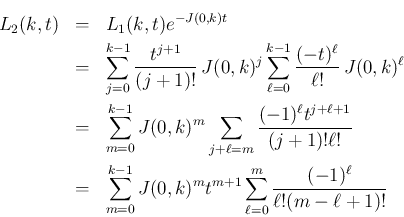
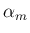 とすると、
とすると、
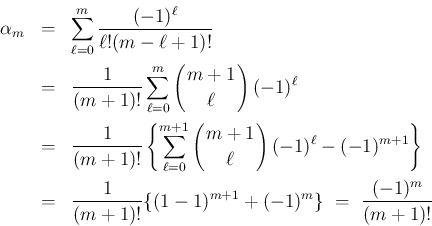
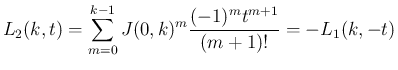
実際は、
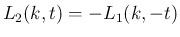 を求めてからそれを
を求めてからそれを 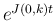 に
かけることは、むしろ直接積分を計算するより面倒なので特に意味はないが、
これを使えば一応統一的に
に
かけることは、むしろ直接積分を計算するより面倒なので特に意味はないが、
これを使えば一応統一的に 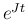 とある行列の積の形にすることができる。
とある行列の積の形にすることができる。
例えば、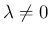 として、
として、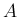 のジョルダン標準形が、
のジョルダン標準形が、
![$\displaystyle J
=\left[\begin{array}{cc}J(\lambda,k_1)&\raisebox{-.5ex}{\Large$0$}\\ [.7ex]
\raisebox{0ex}{\Large$0$}& J(0,k_2)\end{array}\right]
$](img471.png)
![\begin{eqnarray*}\int e^{Jt}dt
&=&
\left[\begin{array}{cc}J(\lambda,k_1)^{-1}...
...\raisebox{0ex}{\Large$0$}& -L_1(k_2,-t)\end{array}\right]e^{Jt}+C\end{eqnarray*}](img472.png)
![\begin{eqnarray*}\int e^{At}dt
&=&
Q\left[\begin{array}{cc}J(\lambda,k_1)^{-1}...
..._2,-t)\end{array}\right]Q^{-1}e^{At}+C
\ =\
\hat{A}(t)e^{At}+C\end{eqnarray*}](img473.png)
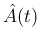 は定数ではなく、
0 の固有値の部分は
は定数ではなく、
0 の固有値の部分は 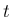 の多項式を含むところが異なる。
より一般のジョルダン標準形の場合も同様である。
竹野茂治@新潟工科大学
の多項式を含むところが異なる。
より一般のジョルダン標準形の場合も同様である。
竹野茂治@新潟工科大学