2 sin x, cos x の微分
まず、関数 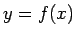 の導関数の定義は
の導関数の定義は
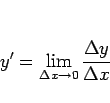
である。ここで、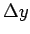 は
は 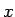 の増加分
の増加分 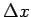 に対する
に対する
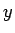 の増加分を表していて、
の増加分を表していて、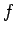 を使って書き表すと、
を使って書き表すと、
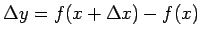 となる。
となる。
さて、三角関数 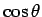 、
、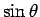 (
(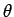 の単位はラジアン)
の値は、単位円の中心角
の単位はラジアン)
の値は、単位円の中心角 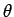 に対する円周上の点の
に対する円周上の点の 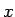 座標と
座標と 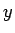 座標で
与えられることを思い出す (図 1)。
座標で
与えられることを思い出す (図 1)。
図 1:
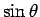 ,
,
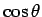 と単位円
と単位円
|
|
よって、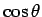 、
、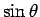 の導関数は、それぞれ
の導関数は、それぞれ
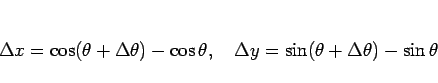
と 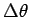 との比の極限によって得られる (図 2):
との比の極限によって得られる (図 2):
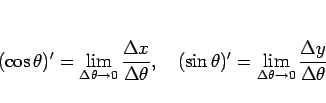
図 2 上では
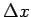 は
は 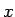 方向の移動幅 (負の値)、
方向の移動幅 (負の値)、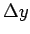 は
は 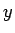 方向の移動幅
として表されていて、
方向の移動幅
として表されていて、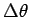 は角度変化分であるが、弧度法の角度と
弧の長さの関係から、
は角度変化分であるが、弧度法の角度と
弧の長さの関係から、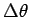 は移動した分の弧の長さにも
等しいことがわかる。
は移動した分の弧の長さにも
等しいことがわかる。
そして、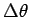 を 0 に近づけて行くとき、
を 0 に近づけて行くとき、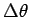 が 0 に
近ければ、この
が 0 に
近ければ、この 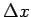 ,
, 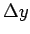 ,
, 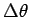 (図 2) は、
弧の部分を、点
(図 2) は、
弧の部分を、点
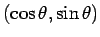 での接線で置き換えた図で
考えたもので近似できる (図 3)。
での接線で置き換えた図で
考えたもので近似できる (図 3)。
この、接線で近似した図 4 の三角形 PQR を考える。
この三角形 PQR は、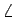 R が直角の直角三角形であり、
R が直角の直角三角形であり、
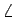 P は
P は 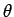 に等しく
に等しく
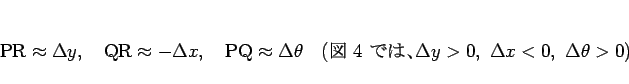
となっている。よって、
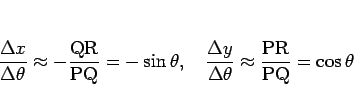 |
(2) |
となり、
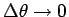 のとき、この近似は厳密に等しい
等号になると考えられる。ゆえに
のとき、この近似は厳密に等しい
等号になると考えられる。ゆえに
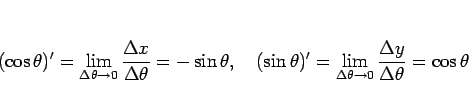
となる。
竹野茂治@新潟工科大学
2014年7月2日
![]() 、
、![]() (
(![]() の単位はラジアン)
の値は、単位円の中心角
の単位はラジアン)
の値は、単位円の中心角 ![]() に対する円周上の点の
に対する円周上の点の ![]() 座標と
座標と ![]() 座標で
与えられることを思い出す (図 1)。
座標で
与えられることを思い出す (図 1)。
![]() 、
、![]() の導関数は、それぞれ
の導関数は、それぞれ
![]() を 0 に近づけて行くとき、
を 0 に近づけて行くとき、![]() が 0 に
近ければ、この
が 0 に
近ければ、この ![]() ,
, ![]() ,
, ![]() (図 2) は、
弧の部分を、点
(図 2) は、
弧の部分を、点
![]() での接線で置き換えた図で
考えたもので近似できる (図 3)。
での接線で置き換えた図で
考えたもので近似できる (図 3)。