3 平均が満たすべき条件
本節では、各平均値に以下のように名前をつけ、
それらが満たすべき条件を見ていくことにする:
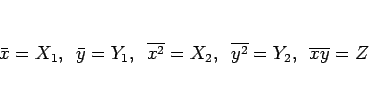 |
(7) |
まず、(2), (3) の定義より
これらは非負の値なので、
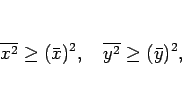
すなわち
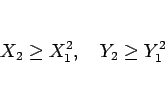 |
(8) |
の関係が成り立つ。
これらは、以下のようにシュワルツの不等式から導くこともできる:
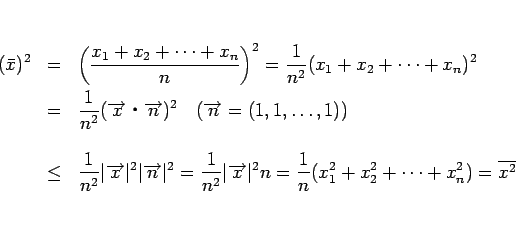
同じように、シュワルツの不等式より、
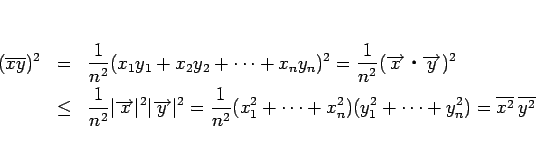
となるので、
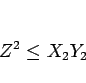 |
(9) |
の関係が成り立つことがわかる。
さらに、(4) の 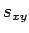 の定義式にシュワルツの不等式を用いると、
の定義式にシュワルツの不等式を用いると、
となるので、
これに (2), (3), (4) の
右辺の式を代入して平均の式に置き換えると
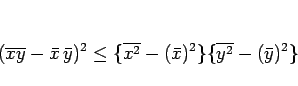
となり、よって
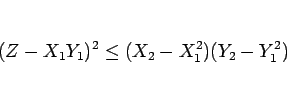 |
(11) |
の関係が成り立つことになる。
なお、この (10) の関係は、相関係数 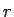 が
が
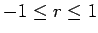 を満たすことを意味している。
を満たすことを意味している。
竹野茂治@新潟工科大学
2014年11月18日
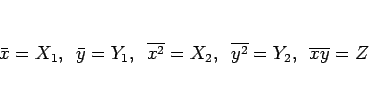
![]() の定義式にシュワルツの不等式を用いると、
の定義式にシュワルツの不等式を用いると、
![]() が
が
![]() を満たすことを意味している。
を満たすことを意味している。