|
|
(1) |
以下に上げる公式は基本的なものであり、 ラプラス変換に関する教科書 (例えば [1]) であればたいてい載っている。
[f (t)] =
[f (t)](s) =
e-stf (t)dt
(1)
| 線形性 | (2) | ||
| eat 倍 | (3) | ||
| t 倍 | (4) | ||
| 微分 | (5) | ||
| スケール変換 | (6) |
| = | |||
| = |
具体的な関数のラプラス変換については、以下のものを証明なしにあげておく。 詳細は、教科書等 (例えば [1]) を参照のこと。
| f | 1 | tk | sin t | cos t |
|
|
|
|
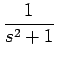
|
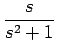
|
ラプラス変換は、次の意味で一対一であることが保証されている。
f (t)
, g(t)
が t > 0
で連続で、
![]() [f](s)
と
[f](s)
と
![]() [g](s)
が同じ関数であれば、
f (t)
と g(t)
も等しい。
[g](s)
が同じ関数であれば、
f (t)
と g(t)
も等しい。
これにより、変換後の関数から変換前の関数への対応も考えることができ、
それがラプラス逆変換である:
この F(s) のラプラス逆変換を求めるには、 例えば以下のような方法がある。
-1[F(s)](t) = f (t)

[f (t)](s) = F(s)
を計算する
-1[F(s)](t) =
estF(s)ds
最初のものは、逆変換を陽に表わす積分公式なのであるが、 その計算は易しくはないためあまり用いられず、 通常の計算、多くの工学向けの教科書では 2 つ目のものがよく用いられるようである。
その方法とは例えば、
のラプラス逆変換を考えると、(2), (3) より
F(s) =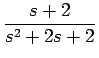
| F(s) | = | 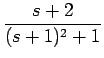 = = 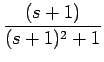 + + 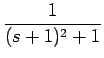 |
|
| = |  + + 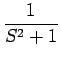 ![$\displaystyle \left.\vphantom{\frac{S}{S^2+1}+\frac{1}{S^2+1}}\right]_{{S=s+1}}^{}$](img24.gif) = = |
||
| = |
となる、といった具合である。
-1[F(s)] = e-tcos t + e-tsin t
本稿では、分子の次数が分母の次数よりも小さい有理関数
(A, B は s の多項式、deg A は A の次数) の ラプラス逆変換を求めることを目標とする。 多項式、三角関数 (sin , cos )、指数関数の和や積のラプラス変換は 必ずこの形になり、 また逆にこの形の関数 F(s) のラプラス逆変換は、 多項式、三角関数、指数関数の和と積で表される。 本稿ではその事実、および計算方法について解説していく。
F(s) =(deg A(s) < deg B(s))
竹野茂治@新潟工科大学