sin t = 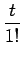 -
- 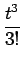 +
+ 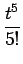 -
- 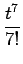 + ...
+ ...
sin t のマクローリン展開は、
であり、これはすべての実数 t で成り立つ。よって、
sin t =-
+
-
+ ...
となる。
t sin t = -
+
-
+ ...
(6)
| = | |||
| = |
とすれば、
h(X) = 2X - 4X3 +6X5 -8X7 + ... (7)
と書けることになる。ところで、(8) は
[t sin t] =
h
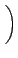
を微分したものであり、(9) は初項 (- 1) 、公比 (- X2) の 等比級数なので、
H(X) = - 1 + X2 - X4 + X6 - X8 + ... (8)
となる。よって、
H(X) =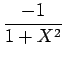
より、
h(X) = H'(X) ==
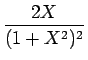
| = | 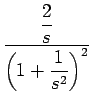 = = 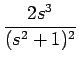 = = 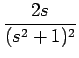 |
竹野茂治@新潟工科大学