B.3 エントロピー条件

4.2 節と同様の計算を 式 (B.5) に対して行うと、

$$\begin{eqnarray*}0 &=& -\int_a^b\eta(U(t_0,x))dx+\int_{X_1}^{X_2}\eta(U(t_1,x... ...gr]_{X(t;t_0,a)}^{X(t;t_0,b)}dt \\ && +\int_{t_0}^{t_1}\Phi dt\end{eqnarray*}$$

となることがわかる。 特に、 $(\eta,q)=(\rho S,\rho uS)$ のように $q-u\eta=0$ 場合は 3 項目の積分は消えるので、

$$\int_{X_1}^{X_2}\eta(U(t_1,x))dx =\int_a^b\eta(U(t_0,x))dx-\int_{t_0}^{t_1}\Phi dt$$ (B.128)

となり、 $\eta$ が凸 (または凹) ならば $\Phi$ は正 (または負) となるので、 エントロピーの総量は減少 (または増加) することになる。 $\eta=\rho S$ は実は凹なので (B.4 節参照)、 (B.8) はエントロピー増大という 熱力学第 2 法則を意味する。

ここからの類推として、弱解にも同様の条件、 すなわち凸なエントロピーに対して 「エントロピーの総量が減少していること」 を課すのがエントロピー条件である ($\rho S$ は凹なので、$\rho S$ とは逆になることに注意)。

しかし、一般の $L^1_{loc}(Q)$ の関数に対して、線積分

$$\int_{X_1}^{X_2}\eta(U(t_1,x))dx$$

の形で条件を課すのはあまり都合がよくないので、弱い意味で、

$$\eta(U)_t+q(U)_x\leq 0$$

を満たすこと、すなわち、

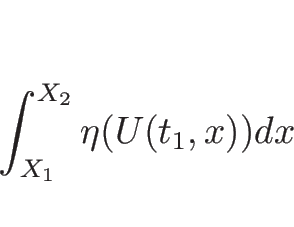
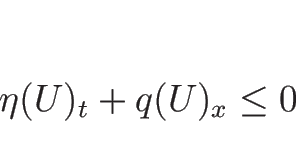
「凸なエントロピー関数を持つ任意のエントロピー対と 任意の非負なテスト関数 $\phi\in C_0^1(Q)$ に対して

$$\int\!\!\!\int _Q\{\eta(U)\phi_t+q(U)\phi_x\}dxdt\geq 0$$ (B.129)

を満たすこと」

を、エントロピー条件 (entropy condition) と呼ぶ。

保存則の一般的な解の存在定理では、 通常ラックス条件の代わりにこの条件が用いられる。 この形の条件であれば、単純な不連続性の関数でなく、 もっと一般の $L^1_{loc}(Q)$ の関数に対して適用できる。

以下に、簡単な場合についてこの条件を考えてみる。

解 $U$ が滑らかな部分では、$\eta_t+q_x=0$ となるので、 もちろんエントロピー条件は満たされる。

$U$ が不連続線 $d=d(t)$ の両側で滑らかな場合は、 条件 (B.9) は、 A 節の図 A.3 のように分けて計算すれば、

$$\begin{eqnarray*}0 &\leq & \int\!\!\!\int _Q\{\eta(U)\phi_t+q(U)\phi_x\}dxdt ... ...q\phi dt) \\ &=& \int_{x=d(t)}\phi(t,d(t))\{[\eta]d'(t)-[q]\}dt\end{eqnarray*}$$

となるので、$\phi$ の任意性より、 $\Phi=d'(t)[\eta]-[q]$ が各 $t$ で 0 以上でなければならないことになる。 よって B.2 節の結果より、 接触不連続の場合は無条件、 衝撃波の場合はラックス条件を満たす衝撃波のみが許されることになる。