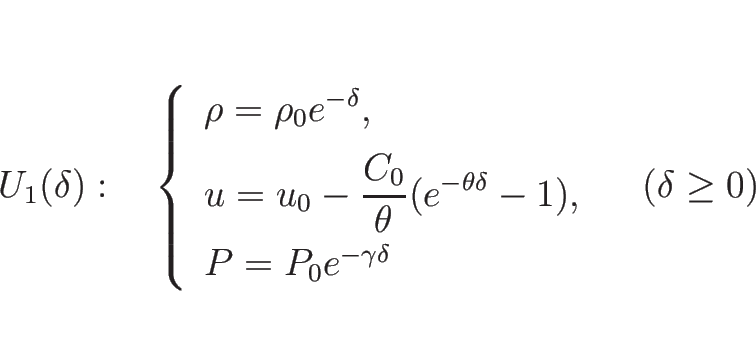
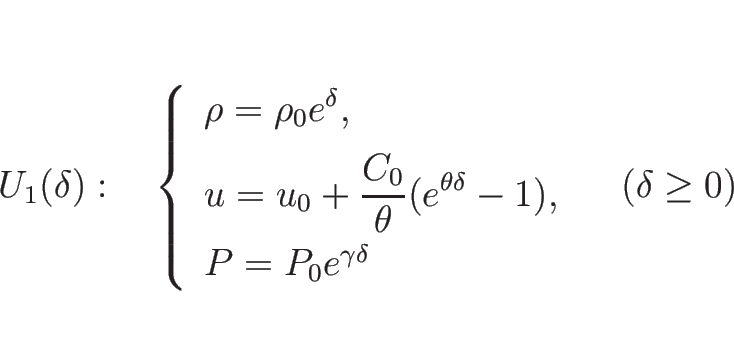
また、4.8 節の結果より、
1-衝撃波曲線 ![]() は
は
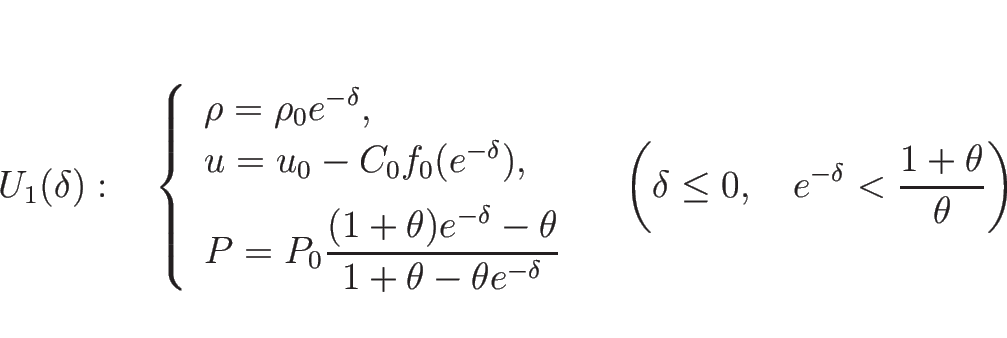
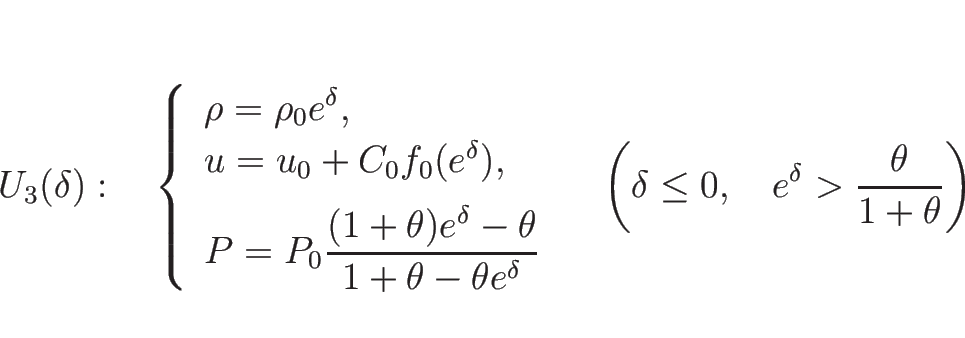
2-接触不連続 ![]() は、
は、
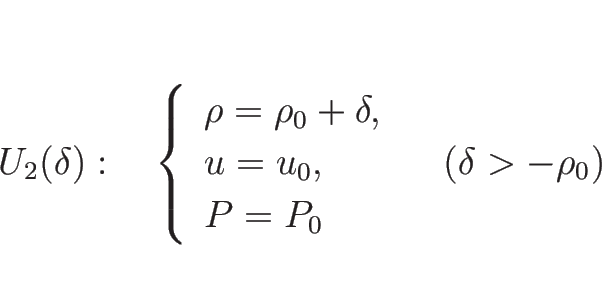
![]() ,
, ![]() を
を
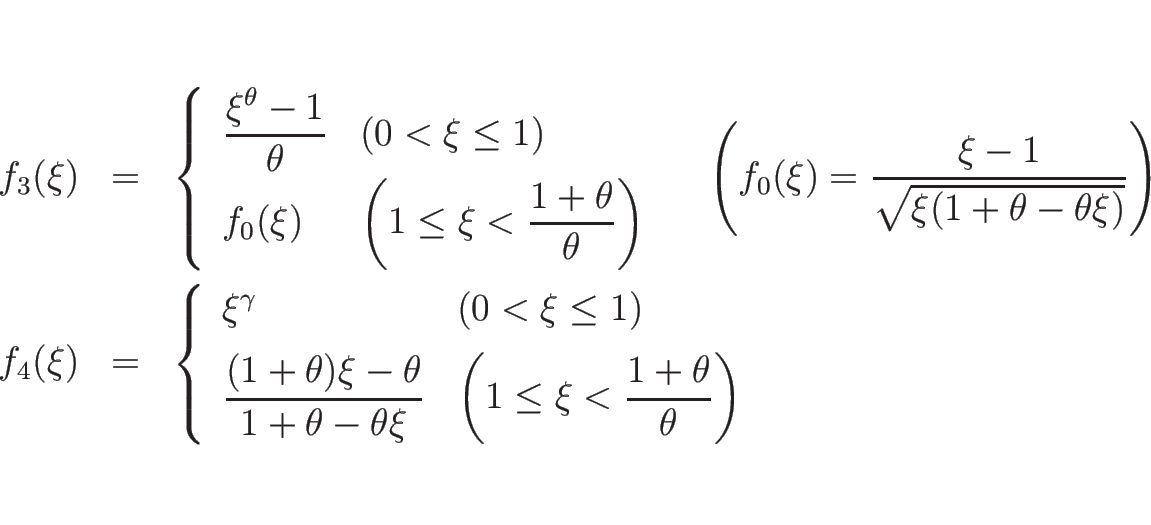
同様に、
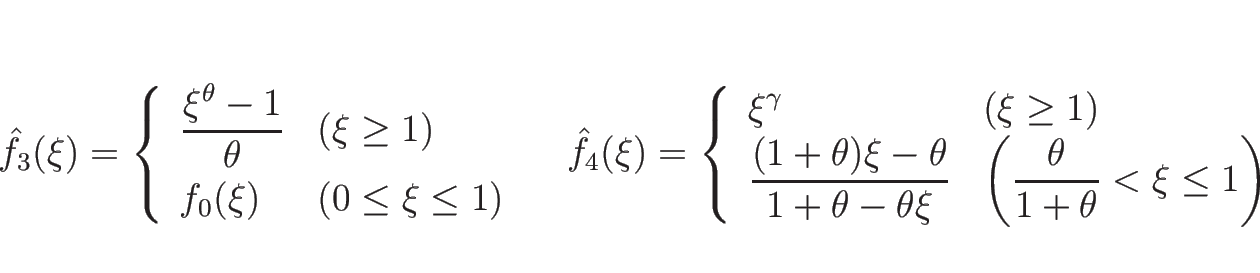
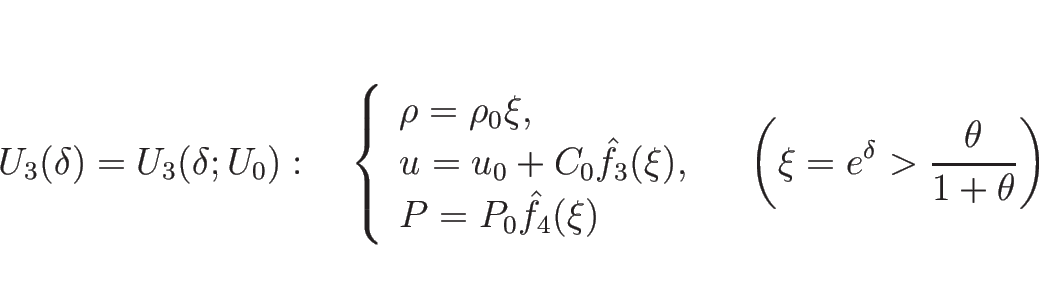
リーマン問題の解は、定理 5.2 の証明のように、
これらが求まれば、
例えば ![]() ならば、
ならば、![]() と
と ![]() は 1-膨張波によってつながり、
その部分の解
は 1-膨張波によってつながり、
その部分の解 ![]() は
は
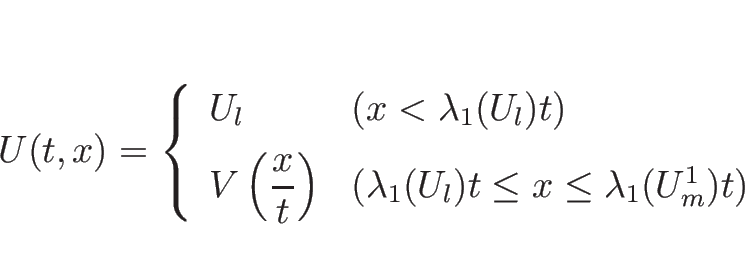
![]() ならば、
ならば、![]() と
と ![]() は 1-衝撃波によってつながり、
その部分の解
は 1-衝撃波によってつながり、
その部分の解 ![]() は
は
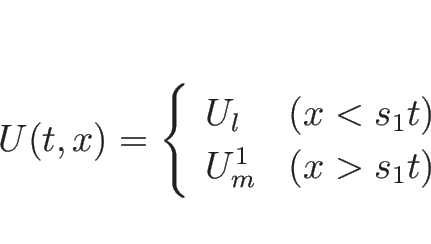
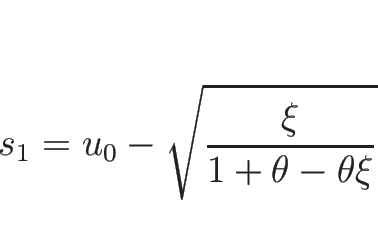
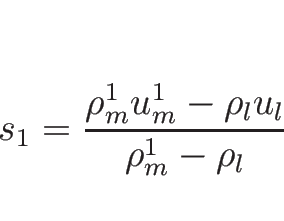
2-単純波 (接触不連続)、3-単純波 (膨張波、または衝撃波) も同様である。
よって、![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() を
求めることが目標となるが、例えば、(5.4) の
を
求めることが目標となるが、例えば、(5.4) の
![]() 成分を見れば
成分を見れば
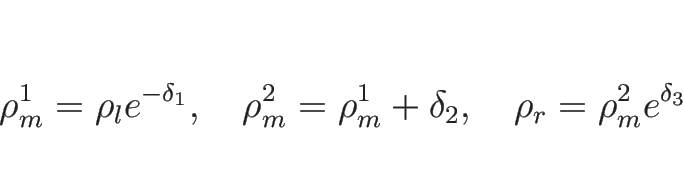
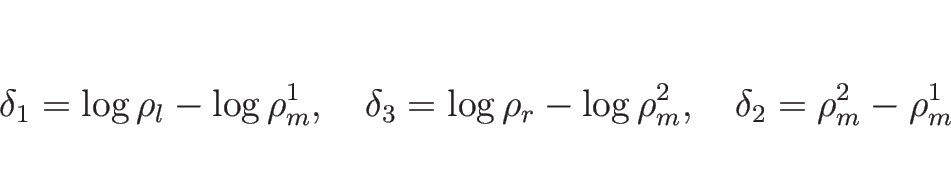
つまり、
![]() ,
,
![]() ,
,
![]() となる
となる ![]() ,
, ![]() を求めればよいのであるが、
を求めればよいのであるが、
![]() 上
上 ![]() ,
, ![]() は一定なので、
は一定なので、
![\begin{displaymath}
U_m^1=\left[\begin{array}{c}\rho_m^1\\ u_m\\ P_m\end{array}\...
...2=\left[\begin{array}{c}\rho_m^2\\ u_m\\ P_m\end{array}\right]
\end{displaymath}](img1077.png)
今、
![]() を逆に
を逆に ![]() について解いたものを
について解いたものを
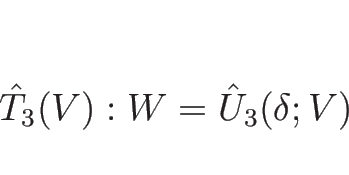
そうすれば、
![\begin{displaymath}
U_m^1=\left[\begin{array}{c}\rho_m^1\\ u_m\\ P_m\end{array}\...
..._m\end{array}\right]=\hat{U}_3(\delta_3;U_r)\ (\hat{T}_3(U_r))
\end{displaymath}](img1082.png)
これを行うために、まず
![]() (
(
![]() )
を式で表わしてみる。
)
を式で表わしてみる。
![]() の場合、
の場合、
![]() は
は
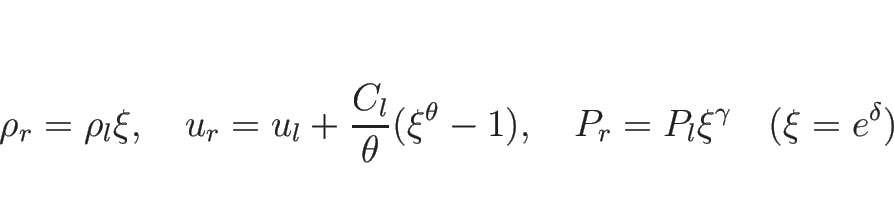
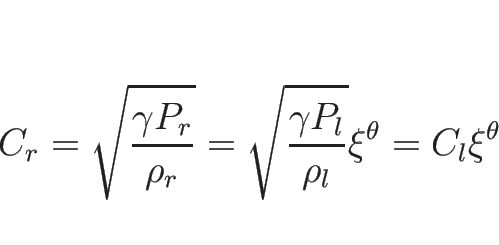
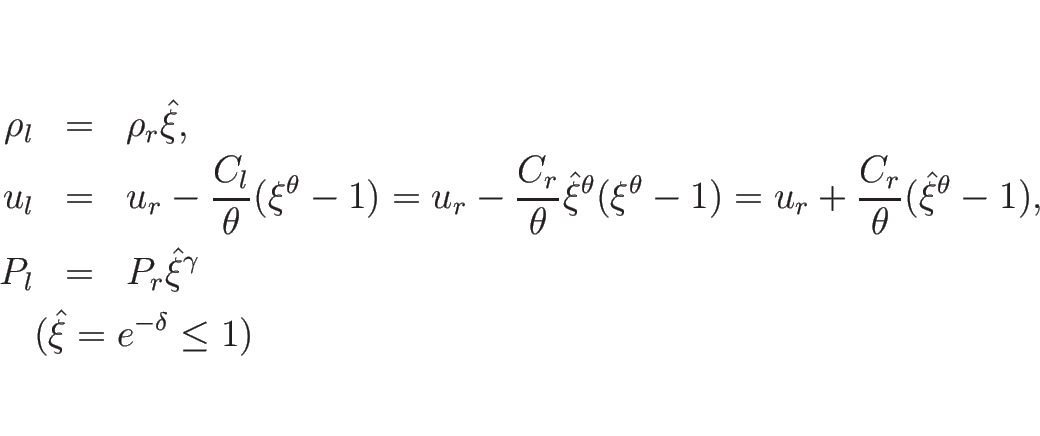
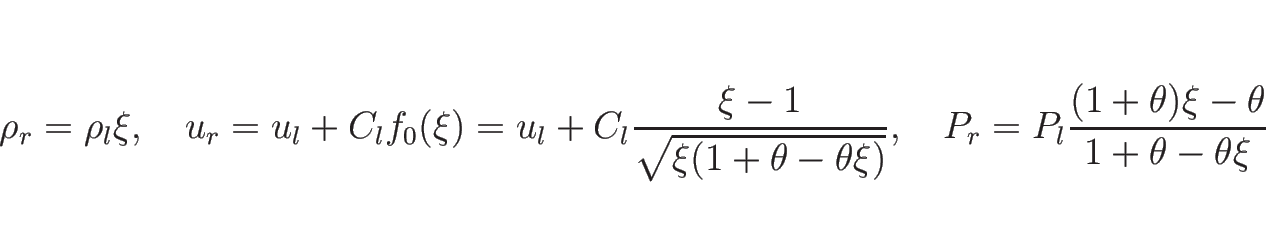
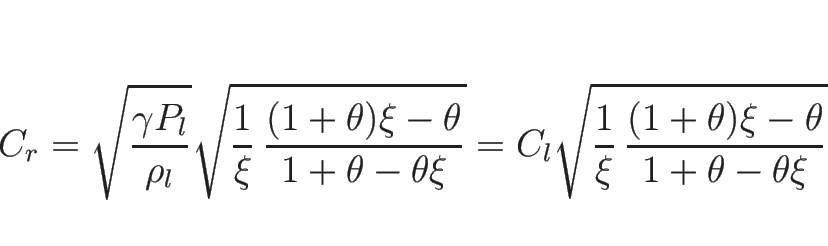
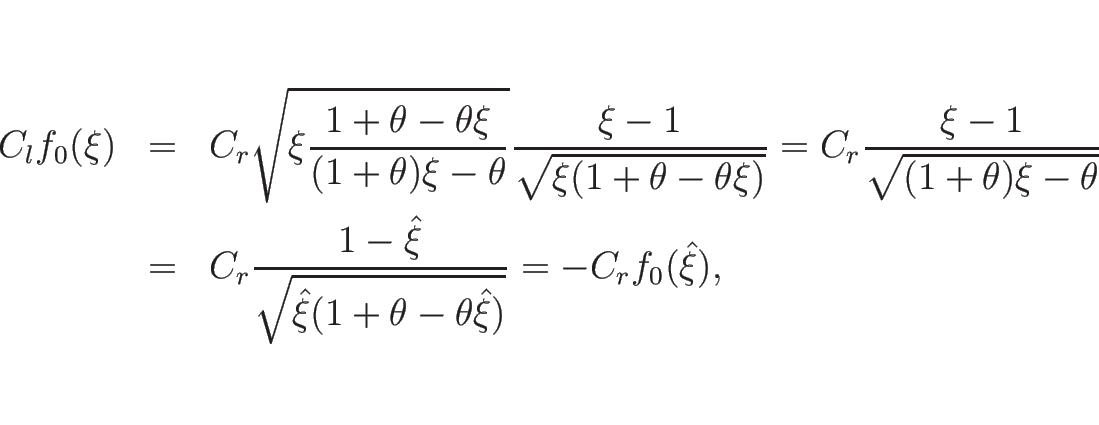
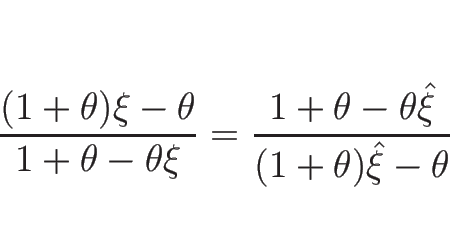
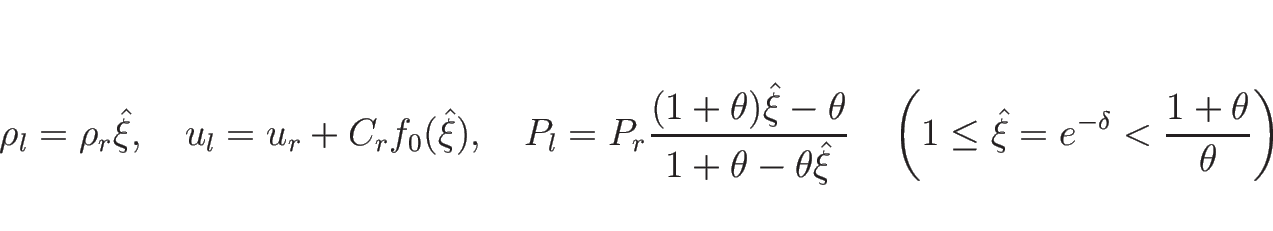
以上をまとめると、![]() をあらためて
をあらためて ![]() と書き直せば、
と書き直せば、
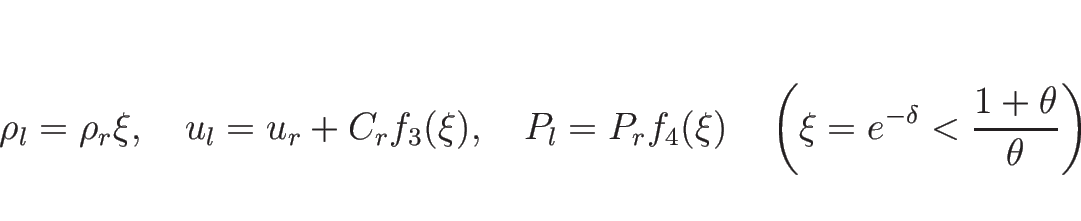
![]() を求めるには、
を求めるには、
![]() 平面への
平面への ![]() と
と
![]() の射影曲線
の射影曲線
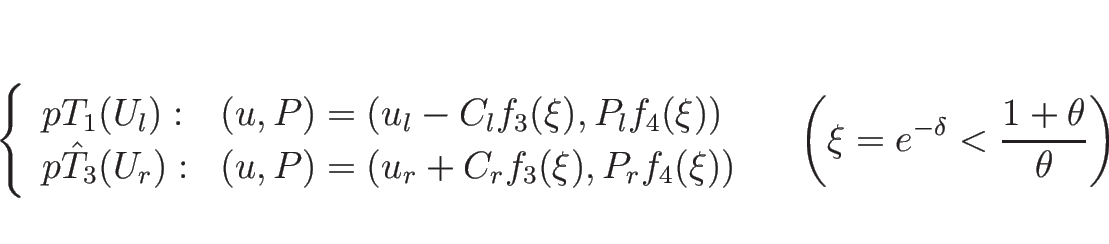
![]() とすると、
とすると、![]() は
は ![]() に関して単調で、
に関して単調で、
![]() のとき
のとき ![]() ,
,
![]() のとき
のとき ![]() なので、
なので、
![]() を
を ![]() の関数
の関数
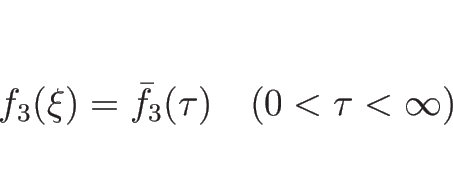
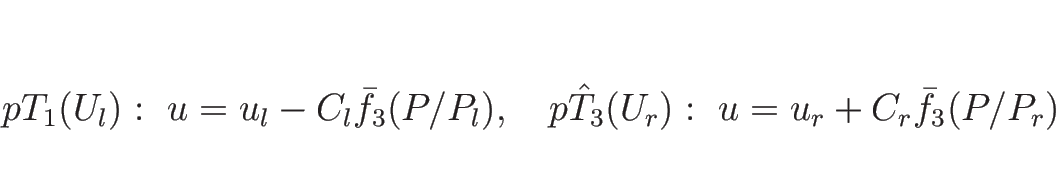
まず ![]() 、すなわち
、すなわち ![]() のときは、
のときは、
![]() より
より
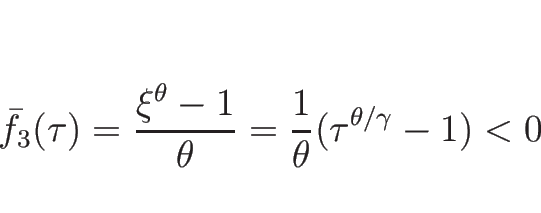
![]() のときは、
のときは、
![]() より、
より、
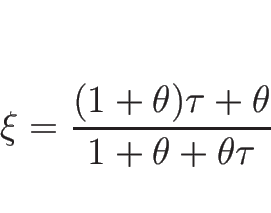
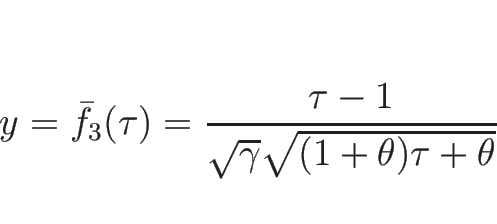
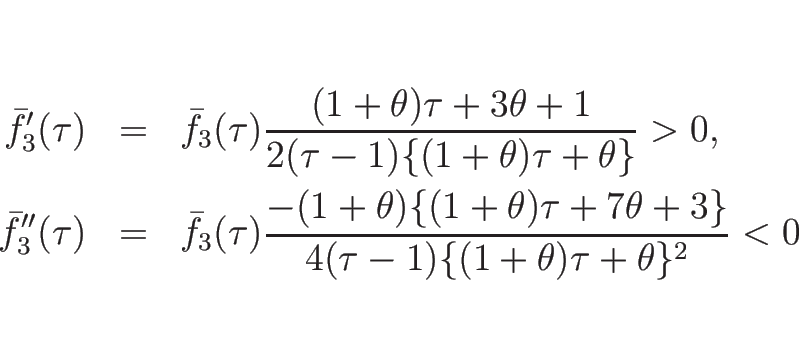
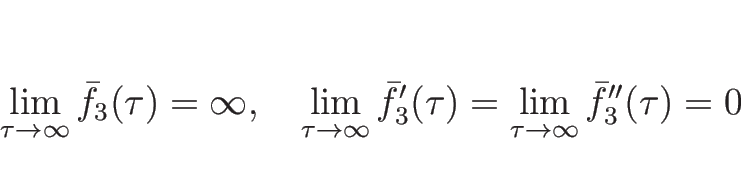
逆に、(5.5) が満たされない場合は、
![]() の領域では 2 つの曲線
の領域では 2 つの曲線 ![]() ,
,
![]() は交わらず、
よって今までの考察のような形ではリーマン問題の解を求めることはできない。
なお、この場合は
は交わらず、
よって今までの考察のような形ではリーマン問題の解を求めることはできない。
なお、この場合は ![]() の両側にある気体の状態
の両側にある気体の状態 ![]() ,
, ![]() が
強く互いに遠ざかろうとしていることを意味していて、
その場合は中間に
が
強く互いに遠ざかろうとしていることを意味していて、
その場合は中間に ![]() ,
, ![]() の状態、
すなわち「真空」が発生する。
真空状態をも解と見なして考える立場もあるが、
通常のリーマン問題の一般論の考察からは外れてしまうので、
ここではそのような話には立ち入らないことにする。
の状態、
すなわち「真空」が発生する。
真空状態をも解と見なして考える立場もあるが、
通常のリーマン問題の一般論の考察からは外れてしまうので、
ここではそのような話には立ち入らないことにする。
竹野茂治@新潟工科大学