4 平均自乗誤差
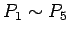 と
と 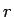 との近さをはかる尺度として、
誤差評価でよく用いられる平均自乗誤差を計算してみる。
との近さをはかる尺度として、
誤差評価でよく用いられる平均自乗誤差を計算してみる。
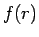 と
と 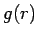 (
(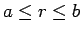 ) の 平均自乗誤差
(以後
) の 平均自乗誤差
(以後 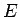 とする) とは、
とする) とは、
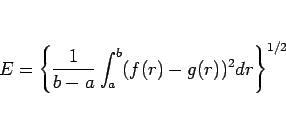
で定義されるものであり、関数解析学では 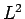 ノルム と呼ばれている3。
これを
ノルム と呼ばれている3。
これを 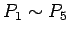 に対して計算してみる。
に対して計算してみる。
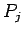 に対する平均自乗誤差を
に対する平均自乗誤差を 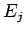 (
(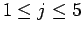 ) とすると、
グラフから、
) とすると、
グラフから、
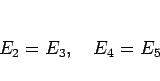
となることが予想されるが、一応すべて計算してみることにする。
まずは 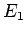 から。
から。
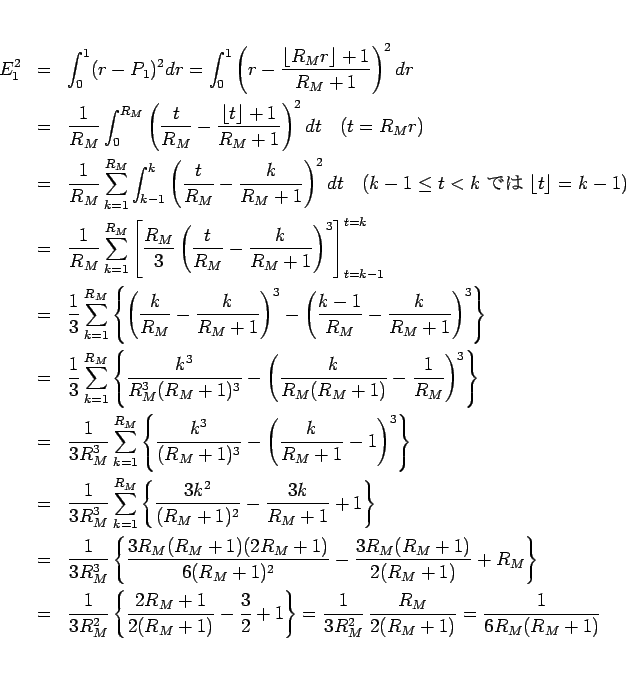
よって、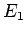 は
は
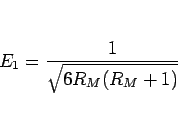
となる。
次に  。
。
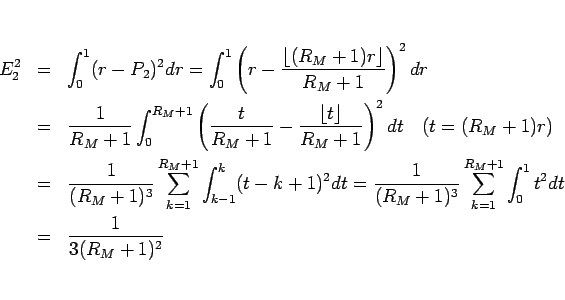
よって、 は
は
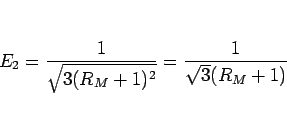
となる。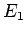 と比較すると、
と比較すると、
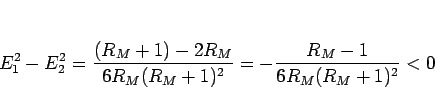
より、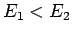 である。
である。
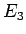 は、
は、
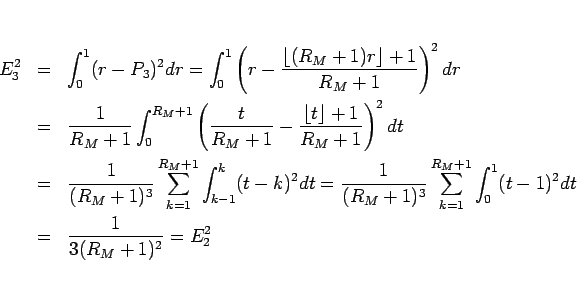
となるので、確かに 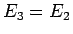 となっている。
となっている。
次は 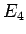 。
。
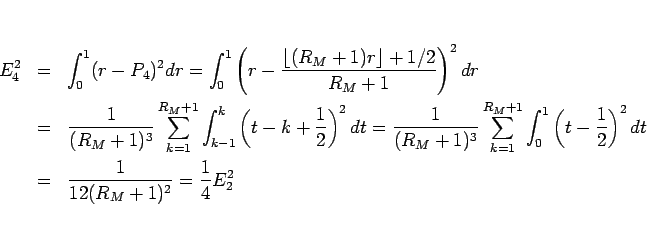
となるので、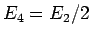 となる。
となる。
最後に 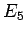 。
。
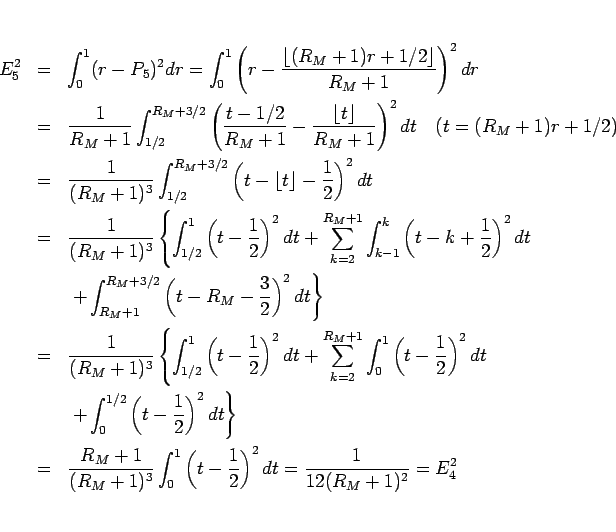
となるので、確かに 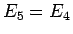 となる。
となる。
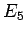 と
と 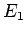 を比較すると、
を比較すると、
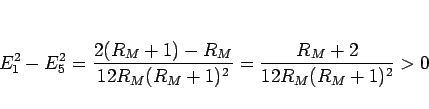
より、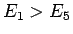 となる。
となる。
よって、結果として、
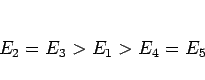
となることがわかる。
竹野茂治@新潟工科大学
2007年5月31日
![]() に対する平均自乗誤差を
に対する平均自乗誤差を ![]() (
(![]() ) とすると、
グラフから、
) とすると、
グラフから、
![]() 。
。
![]() は、
は、
![]() 。
。
![]() 。
。
![]() と
と ![]() を比較すると、
を比較すると、