5 ベッセルの方程式への帰着と境界条件
さて、3 節に戻って、
(10) を満たす 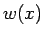 を求めることにする。
それには、方程式 (10) を変数変換して、
ベッセルの微分方程式 (11) に帰着させる。
を求めることにする。
それには、方程式 (10) を変数変換して、
ベッセルの微分方程式 (11) に帰着させる。
今、
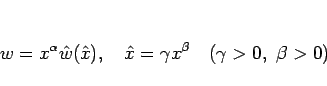 |
(18) |
とすると、
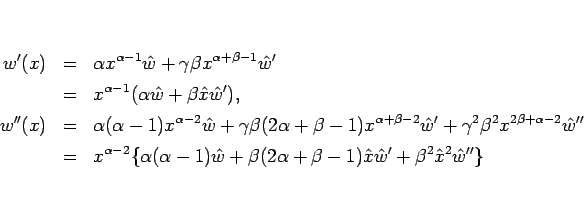
となるので、これらを (10) に代入して整理すると、
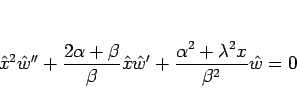 |
(19) |
が得られる。よって、
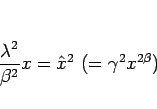
となるように 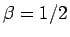 ,
,
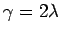 とし、
とし、
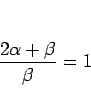
となるように、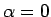 とすると、
(19) は
とすると、
(19) は 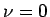 のベッセルの方程式となる。
よって、この
のベッセルの方程式となる。
よって、この 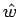 は、4 節に述べたように
は、4 節に述べたように
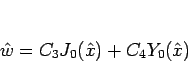
と書けるので、元の 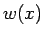 に戻すと、
に戻すと、
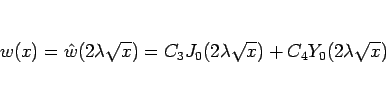 |
(20) |
となる。
この 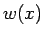 は、もちろん
は、もちろん 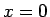 では有界である必要があるが、
4 節に述べたように
では有界である必要があるが、
4 節に述べたように 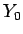 は
は 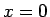 で有界ではないので、
で有界ではないので、
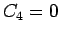 でなければならない。
よって、
でなければならない。
よって、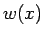 は
は 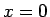 での境界条件がないまま (厳密には、「
での境界条件がないまま (厳密には、「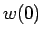 は有限である」という境界条件によって)、
1 つの任意定数が決定されて、
は有限である」という境界条件によって)、
1 つの任意定数が決定されて、
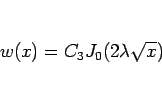
となる。これを 3 節の 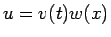 に戻せば、
に戻せば、
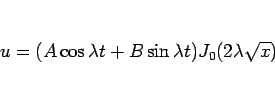 |
(21) |
と書ける。
さて、この (21) が、境界条件 (3) を満たすためには、
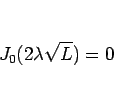
すなわち、
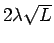 が
が 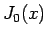 の零点である必要がある。
よって 4 節の (16) により、
の零点である必要がある。
よって 4 節の (16) により、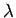 は
は
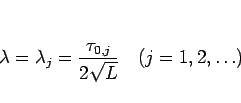
という離散的な値のいずれかであることになる。
方程式 (8) は線形であるから、
この 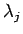 に対する (21) の重ね合わせ
に対する (21) の重ね合わせ
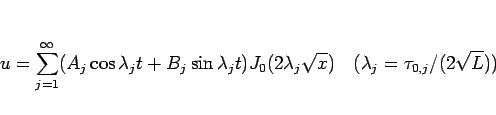 |
(22) |
も (8) の解となる。
これが初期条件 (2) を満たすとすると
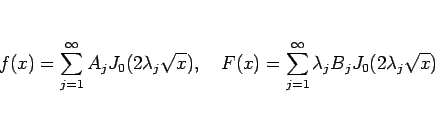 |
(23) |
となるが、
4 節のフーリエ・ベッセル展開 (17) により
となり、この 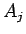 ,
, 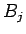 とフーリエ・ベッセル展開の完全性により、
(23) が確かに
とフーリエ・ベッセル展開の完全性により、
(23) が確かに 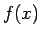 ,
, 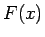 を表すことがわかる。
よってこの
を表すことがわかる。
よってこの 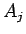 ,
, 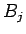 による (22) は、
方程式 (8) の
初期条件 (2) と境界条件 (3) を満たす解となることがわかる。
による (22) は、
方程式 (8) の
初期条件 (2) と境界条件 (3) を満たす解となることがわかる。
つまり、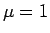 の場合の方程式 (8) は、
の場合の方程式 (8) は、
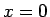 での境界条件 (6) は必要なく
解がちゃんと決定することになり、
これは、
での境界条件 (6) は必要なく
解がちゃんと決定することになり、
これは、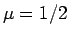 の場合とは状況が異なる。
つまり
の場合とは状況が異なる。
つまり 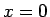 での境界条件 (6) の必要性は、
方程式 (5) の主要部 (4) のみでは決定せず、
低階の項
での境界条件 (6) の必要性は、
方程式 (5) の主要部 (4) のみでは決定せず、
低階の項 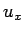 の係数に依存するものであることがわかる。
の係数に依存するものであることがわかる。
竹野茂治@新潟工科大学
2009年6月22日
![]() は、もちろん
は、もちろん ![]() では有界である必要があるが、
4 節に述べたように
では有界である必要があるが、
4 節に述べたように ![]() は
は ![]() で有界ではないので、
で有界ではないので、
![]() でなければならない。
よって、
でなければならない。
よって、![]() は
は ![]() での境界条件がないまま (厳密には、「
での境界条件がないまま (厳密には、「![]() は有限である」という境界条件によって)、
1 つの任意定数が決定されて、
は有限である」という境界条件によって)、
1 つの任意定数が決定されて、
![]() に対する (21) の重ね合わせ
に対する (21) の重ね合わせ
![]() の場合の方程式 (8) は、
の場合の方程式 (8) は、
![]() での境界条件 (6) は必要なく
解がちゃんと決定することになり、
これは、
での境界条件 (6) は必要なく
解がちゃんと決定することになり、
これは、![]() の場合とは状況が異なる。
つまり
の場合とは状況が異なる。
つまり ![]() での境界条件 (6) の必要性は、
方程式 (5) の主要部 (4) のみでは決定せず、
低階の項
での境界条件 (6) の必要性は、
方程式 (5) の主要部 (4) のみでは決定せず、
低階の項 ![]() の係数に依存するものであることがわかる。
の係数に依存するものであることがわかる。