2 μ=1/2 の場合
この節では、(5) が通常の波動方程式に帰着できる 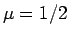 の場合についてまず考察する。
の場合についてまず考察する。
通常の波動方程式
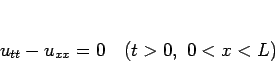 |
(7) |
の場合は、よく知られているように、
初期条件 (2) と境界条件 (3) だけでは足りず、
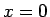 での境界条件 (6) も必要で、
それによりそれらを満たす解の存在と一意性が保証される。
での境界条件 (6) も必要で、
それによりそれらを満たす解の存在と一意性が保証される。
今、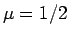 の場合の (5) を考え、
の場合の (5) を考え、
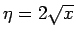 とし、
とし、
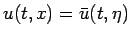 とすると、
とすると、
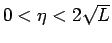 で、
で、
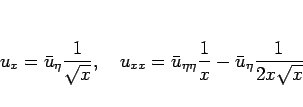
より、
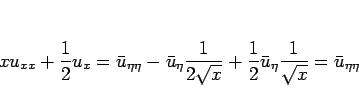
となるので、(2), (3), (5), (6) は、
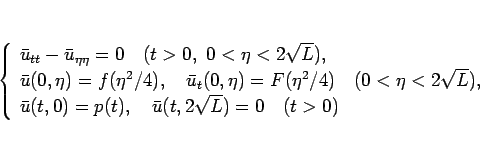
となり、これは通常の波動方程式 (7) の形なので、
これらの初期値境界値によって
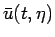 が一意に決まり、
それにより
が一意に決まり、
それにより 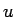 が
が
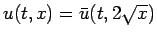 と求まることになる。
と求まることになる。
つまり、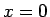 での境界条件 (6) は、
少なくとも
での境界条件 (6) は、
少なくとも 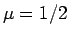 の場合は必要であることになる。
の場合は必要であることになる。
竹野茂治@新潟工科大学
2009年6月22日
![]() の場合の (5) を考え、
の場合の (5) を考え、
![]() とし、
とし、
![]() とすると、
とすると、
![]() で、
で、
![]() での境界条件 (6) は、
少なくとも
での境界条件 (6) は、
少なくとも ![]() の場合は必要であることになる。
の場合は必要であることになる。