5 漸近的な様子
さて、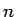 が大きくなると、
が大きくなると、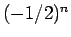 は 0 に収束していくから、
(16), (17) より、
は 0 に収束していくから、
(16), (17) より、
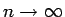 のときに
のときに
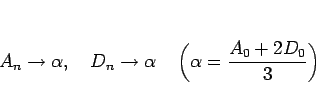
と収束することがわかる。
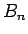 ,
, 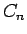 は (18) により、
は (18) により、
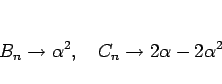
のようになる。
これらの極限を
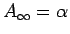 のように書くことにすると、
結局以下のようになる。
のように書くことにすると、
結局以下のようになる。
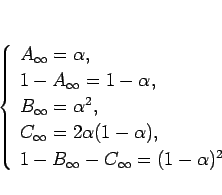 |
(19) |
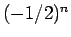 は、かなり速く 0 に近づくので、
数世代でほぼ (19) の値になる。
は、かなり速く 0 に近づくので、
数世代でほぼ (19) の値になる。
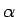 は、
は、
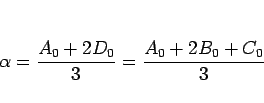 |
(20) |
であり、つまりこの最初の世代の比率で与えられる 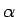 の値によって、
安定的な比率 (19) が決定することになる。
の値によって、
安定的な比率 (19) が決定することになる。
なお、
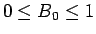 ,
,
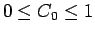 ,
,
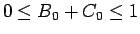 なので、
なので、
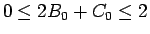 (2 になるのは
(2 になるのは 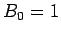 ,
, 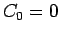 のとき) であり、
のとき) であり、
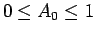 であるから
であるから 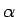 は 0 から 1 までの値を取り得る。
は 0 から 1 までの値を取り得る。
安定的な比率の式 (19) を見ると、
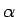 は
は
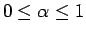 であるから、
であるから、
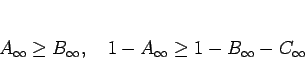
は言える。つまり、男性のその性質を持つ割合 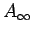 は、
女性のその性質を持つ割合
は、
女性のその性質を持つ割合 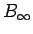 よりは確かに多くなる。
しかし、その他の大小関係は、
よりは確かに多くなる。
しかし、その他の大小関係は、
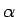 の値によって色々な上下はありえて、
グラフを書いてみればわかるが、
それらは
の値によって色々な上下はありえて、
グラフを書いてみればわかるが、
それらは
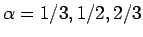 でそれぞれ大小が変化する。
例えば
でそれぞれ大小が変化する。
例えば 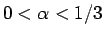 であれば、
であれば、
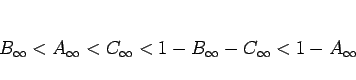
のようになる。
元々の話の場合は、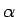 が 0 に近い場合であるが、
この場合は
が 0 に近い場合であるが、
この場合は 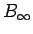 は 2 次なのでかなり小さくなる。
例えば
は 2 次なのでかなり小さくなる。
例えば
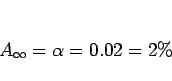
であったとすると、
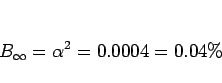
であるから、確かに女性のその性質を持つ割合は、
男性に比べてはるかに小さくなる。
ただし、この場合は
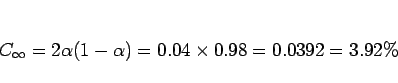
となるので、女性のうち潜在的にその因子を持つ割合 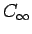 は、
は、
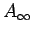 の倍位いることになる。
の倍位いることになる。
竹野茂治@新潟工科大学
2007年9月4日
![]() は、かなり速く 0 に近づくので、
数世代でほぼ (19) の値になる。
は、かなり速く 0 に近づくので、
数世代でほぼ (19) の値になる。
![]() は、
は、
![]() ,
,
![]() ,
,
![]() なので、
なので、
![]() (2 になるのは
(2 になるのは ![]() ,
, ![]() のとき) であり、
のとき) であり、
![]() であるから
であるから ![]() は 0 から 1 までの値を取り得る。
は 0 から 1 までの値を取り得る。
![]() は
は
![]() であるから、
であるから、
![]() が 0 に近い場合であるが、
この場合は
が 0 に近い場合であるが、
この場合は ![]() は 2 次なのでかなり小さくなる。
例えば
は 2 次なのでかなり小さくなる。
例えば