10 摩擦や空気抵抗がある場合
後は、元の問題の状況が少し変わった場合、例えば摩擦を考慮した場合、
空気抵抗がある場合、初速度が 0 でない場合、
そしてすべる場合ではなくむしろ実際は多いと思われる
玉などをころがらせる場合について考えてみる。
まず本節では、摩擦や空気抵抗がある場合について考察する。
摩擦がある場合については、[8] のサイトには、
「近似的」な方程式の解析解が書かれているが、
厳密には以下のようになる。
この場合は、動摩擦力
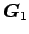 を (1) の式に
追加する必要があるが、動摩擦力は斜面の接線方向で運動の逆方向に働き、
その大きさは斜面からの垂直抗力に比例する。よって、
を (1) の式に
追加する必要があるが、動摩擦力は斜面の接線方向で運動の逆方向に働き、
その大きさは斜面からの垂直抗力に比例する。よって、
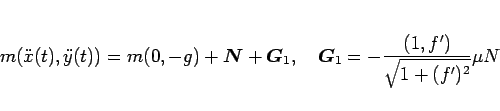 |
(60) |
となる。ここで、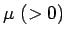 は動摩擦係数である。
よって、各成分に分離すると、
は動摩擦係数である。
よって、各成分に分離すると、
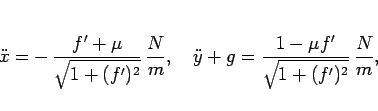 |
(61) |
となる。
[8] では、垂直抗力の大きさ 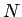 が、
重力の斜面の垂直成分に等しい:
が、
重力の斜面の垂直成分に等しい:
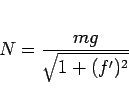 |
(62) |
と仮定して解析解を導いているが、
(62) は厳密には成り立たない。
もし、斜面が直線で、物体の加速度が斜面の接線方向に等しければ、
(62) が成り立つが、
今考えている斜面は直線ではないので、
加速度は斜面の接線方向とは限らず、実際にはこうはならない。
さて、(61) から 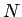 を消去すると、
を消去すると、
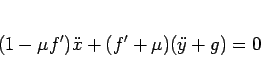 |
(63) |
となる。変分法にかけるためには、この (63) を
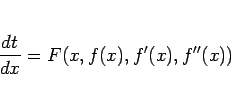
などのような形に直せなくてはいけない。
しかし、(63) は、
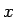 の 2 階の方程式だから 1 回は積分して 1 階の方程式に
直さないといけないだろう。
前のようにエネルギー保存則で考えると、
(63) を
の 2 階の方程式だから 1 回は積分して 1 階の方程式に
直さないといけないだろう。
前のようにエネルギー保存則で考えると、
(63) を 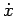 倍して、
倍して、
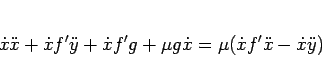
となり、
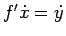 より、
より、
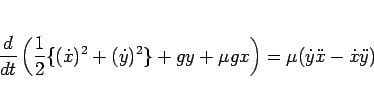 |
(64) |
となる。左辺は 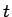 での微分の形になっているが、
右辺はその形にはなっていない。
この右辺の
での微分の形になっているが、
右辺はその形にはなっていない。
この右辺の 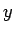 の微分を
の微分を 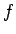 と
と 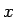 で表すと、
で表すと、
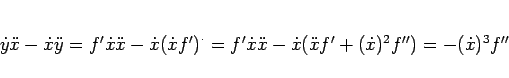
となるが、これもやはり 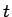 の微分の形に直すことはできない。
の微分の形に直すことはできない。
(63) の式で 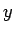 を
を 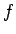 ,
, 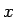 に
書き直してみると、
に
書き直してみると、
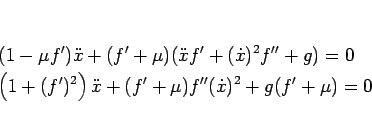
より、
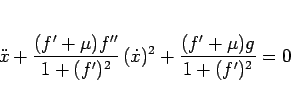 |
(65) |
という 2 階の非線形の微分方程式となる。
これに何らかの積分因子をかけることで、
この式を 1 回積分することは可能かもしれないがかなり難しいだろう。
少なくとも今のところ私には良くわからない。
つまり、摩擦のある場合は、摩擦のない場合の (11) の
式のような、変分法が使える積分の式を導くことも容易ではない。
次は、摩擦の代わりに空気抵抗がある場合について考えてみる。
この場合は (60) の摩擦力
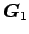 を
空気抵抗力
を
空気抵抗力
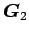 に変えればよい。
に変えればよい。
空気抵抗力
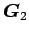 は、運動の逆方向、
すなわち斜面の接線方向で運動の逆方向に
働くところまでは
は、運動の逆方向、
すなわち斜面の接線方向で運動の逆方向に
働くところまでは
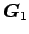 と同じだが、
その大きさは速さ
と同じだが、
その大きさは速さ
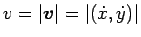 の
関数 (増加関数) と考えることができる。
よく用いられるのは、
速さに比例すると考えた式、あるいは速さの 2 乗に比例すると考えた式である。
ここでは、簡単のため速さに比例するとする。
この場合、
の
関数 (増加関数) と考えることができる。
よく用いられるのは、
速さに比例すると考えた式、あるいは速さの 2 乗に比例すると考えた式である。
ここでは、簡単のため速さに比例するとする。
この場合、
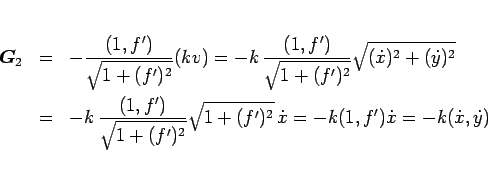
となる。ここで、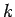 (
(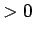 ) は比例定数だが、
抵抗力の大きさが速さに比例するのではない場合は、
) は比例定数だが、
抵抗力の大きさが速さに比例するのではない場合は、
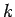 を
を 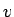 の関数と考えればよい。
の関数と考えればよい。
この場合は、
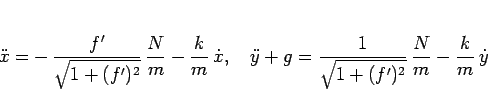 |
(66) |
となるので、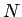 を消去すると、
を消去すると、
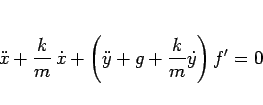 |
(67) |
が得られる。この場合もエネルギーを考えると、
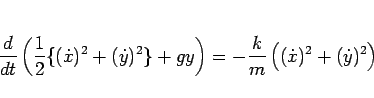 |
(68) |
すなわち、
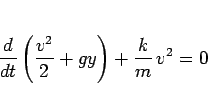 |
(69) |
となるが、これも (64) と同様に
きれいには積分できない。
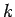 が定数でなく
が定数でなく 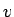 の関数である場合も、
残念ながらあまりうまくいくような気はしない。
の関数である場合も、
残念ながらあまりうまくいくような気はしない。
(67) を 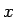 ,
, 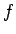 のみの式に書き換えてみると、
のみの式に書き換えてみると、
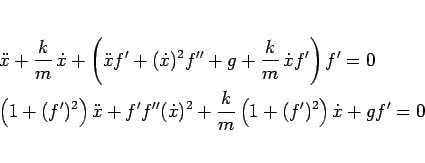
より、
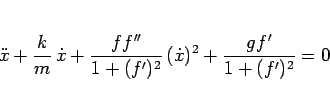 |
(70) |
という 2 階の非線形の微分方程式が得られるが、
これもやはり積分因子を見つけることは容易ではなさそうである。
さらに、摩擦と空気抵抗の両方を考えた式を作ることもできるが、
それも簡単に解けそうな方程式にはならない。
竹野茂治@新潟工科大学
2016年1月8日
![]() を (1) の式に
追加する必要があるが、動摩擦力は斜面の接線方向で運動の逆方向に働き、
その大きさは斜面からの垂直抗力に比例する。よって、
を (1) の式に
追加する必要があるが、動摩擦力は斜面の接線方向で運動の逆方向に働き、
その大きさは斜面からの垂直抗力に比例する。よって、
![]() が、
重力の斜面の垂直成分に等しい:
が、
重力の斜面の垂直成分に等しい:
![]() を消去すると、
を消去すると、
![]() を
を ![]() ,
, ![]() に
書き直してみると、
に
書き直してみると、
![]() を
空気抵抗力
を
空気抵抗力
![]() に変えればよい。
に変えればよい。
![]() は、運動の逆方向、
すなわち斜面の接線方向で運動の逆方向に
働くところまでは
は、運動の逆方向、
すなわち斜面の接線方向で運動の逆方向に
働くところまでは
![]() と同じだが、
その大きさは速さ
と同じだが、
その大きさは速さ
![]() の
関数 (増加関数) と考えることができる。
よく用いられるのは、
速さに比例すると考えた式、あるいは速さの 2 乗に比例すると考えた式である。
ここでは、簡単のため速さに比例するとする。
この場合、
の
関数 (増加関数) と考えることができる。
よく用いられるのは、
速さに比例すると考えた式、あるいは速さの 2 乗に比例すると考えた式である。
ここでは、簡単のため速さに比例するとする。
この場合、
![]() ,
, ![]() のみの式に書き換えてみると、
のみの式に書き換えてみると、