4 変形ベッセル関数の漸近展開
次に、変形ベッセル関数 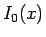 の漸近展開を考える。
の漸近展開を考える。
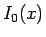 は、次のテイラー展開の形で定義される。
は、次のテイラー展開の形で定義される。
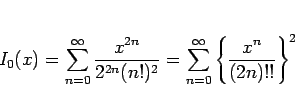 |
(11) |
これは、元々 0 次のベッセル関数
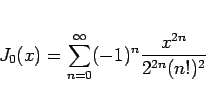
に対し、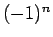 を取ったもの、
すなわち
を取ったもの、
すなわち
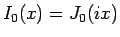 としたものであり、そのため
「変形」ベッセル関数と呼ばれる。
としたものであり、そのため
「変形」ベッセル関数と呼ばれる。
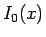 の漸近展開を求めるには (11) のテイラー展開のままでは
難しいので、次のような公式を利用する。
の漸近展開を求めるには (11) のテイラー展開のままでは
難しいので、次のような公式を利用する。
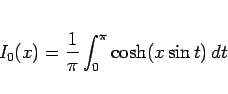 |
(12) |
まず、この公式が成り立つことを示そう。
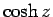 のマクローリン展開は、
のマクローリン展開は、
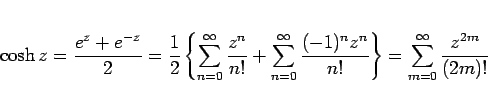
であるから、(12) の右辺は、
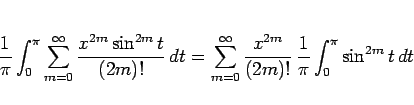 |
(13) |
となる。ここで、
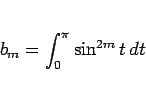
とすると、部分積分により、
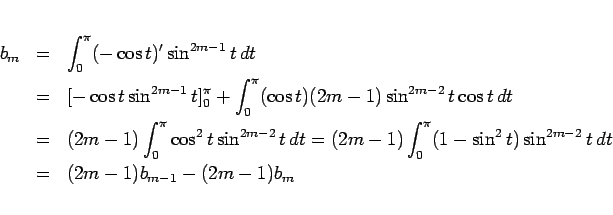
となるから、
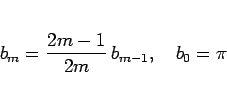
となる。よって、
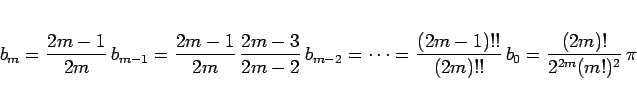
が得られる。これを (13) の右辺に代入すれば (11) になるので、(12) が示されたことになる。
さて、(12) は、
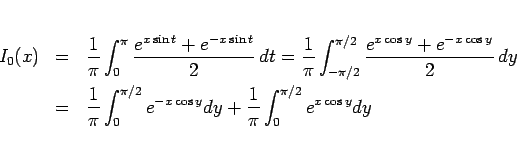
と書き直すこともできるので、よって、
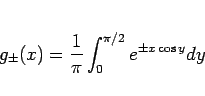
とし、この 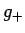 ,
, 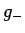 , それぞれの漸近展開を求めることにする。
なお、明らかに
, それぞれの漸近展開を求めることにする。
なお、明らかに 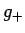 の方が
の方が 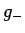 より大きいので、
より大きいので、
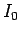 の主要な展開項は
の主要な展開項は 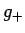 の方であることが予想される。
の方であることが予想される。
まず、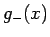 を考えよう。
を考えよう。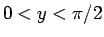 では
では 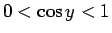 だから、
だから、
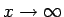 のとき、
のとき、
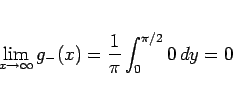
となることがわかる。
よって、この 0 への収束の速さ (オーダー) をまず考えてみる。
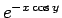 の 1 への収束は、
の 1 への収束は、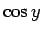 が 0 に近い程遅くなる。
つまりその近くが最も大きな項を与えると予想される。
よって
が 0 に近い程遅くなる。
つまりその近くが最も大きな項を与えると予想される。
よって 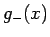 をさらに 2 つに分け、
をさらに 2 つに分け、
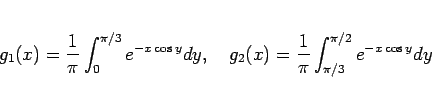
とすると、この 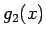 の方が主要部となる。
なお、
の方が主要部となる。
なお、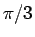 自体にはあまり意味はなく、
自体にはあまり意味はなく、
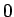 から
から 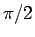 のどこで分けても構わない。
のどこで分けても構わない。
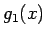 では、
では、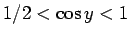 であるから、
であるから、
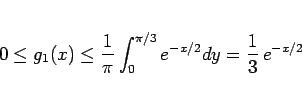 |
(14) |
となるので、
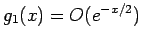 となる。
となる。
一方 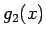 の方は、
の方は、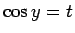 とすると、
とすると、
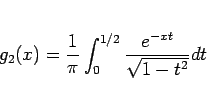
となるが、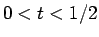 では
では
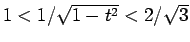 であるので、
であるので、
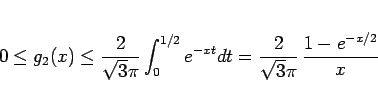
となるから、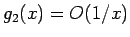 であることがわかる。
であることがわかる。
つまり、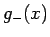 の最も大きい項は
の最も大きい項は 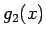 の
の 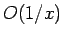 の項
だろうと予想される。
実際、部分積分により、
の項
だろうと予想される。
実際、部分積分により、
となり、よって
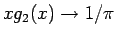 となることがわかる。
一方、(14) より
となることがわかる。
一方、(14) より
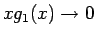 であるから、
よって
であるから、
よって 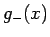 の第 1 近似は、
の第 1 近似は、
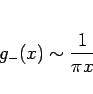
となる。
次に第 2 近似を考える。
(15) で
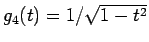 とすると、
再び部分積分により、
とすると、
再び部分積分により、
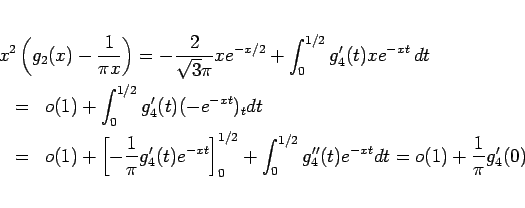
となるから、これと (14) より
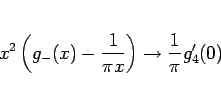
となることがわかる。よって、
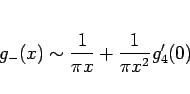
となる。これを繰り返せば、結局
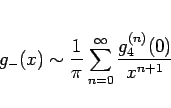 |
(16) |
であることがわかる。
よって後は 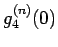 を求めればよいが、一般二項定理を用いれば、
を求めればよいが、一般二項定理を用いれば、
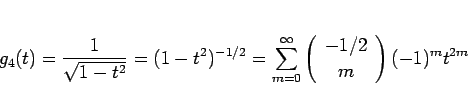
となるので、
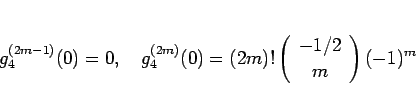
がわかる。ここで、二項係数は
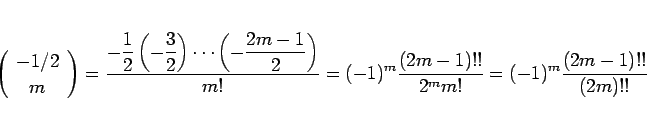
となるので、
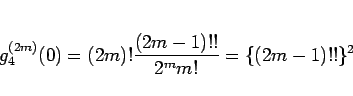
となり、(16) より結局 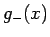 の漸近展開は、
の漸近展開は、
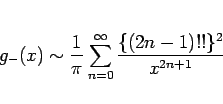 |
(17) |
であることがわかる。
次に、むしろ 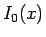 の主要項である
の主要項である 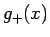 の方を考える。
の方を考える。
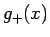 は、
は、
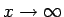 のときに明らかに無限大に発散するが、
のときに明らかに無限大に発散するが、
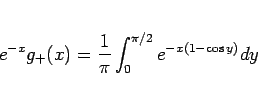 |
(18) |
は、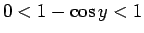 より 0 に収束する。
よって、
より 0 に収束する。
よって、
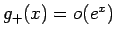 であるから、
まずこの
であるから、
まずこの
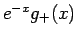 の 0 への収束オーダーを考えてみる。
の 0 への収束オーダーを考えてみる。
今、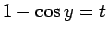 とすると、
とすると、
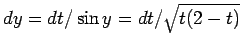 であるから、
であるから、
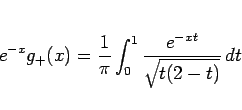
となるが、
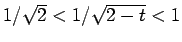 なので、
なので、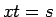 とすれば、
とすれば、
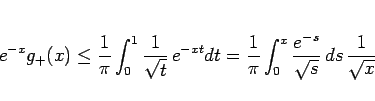
となり、さらに 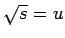 とすると、
とすると、
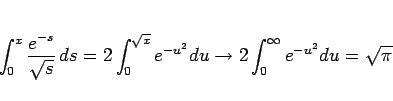
であるから、
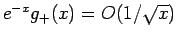 となる。
よって、
となる。
よって、
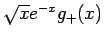 の極限を考えてみよう。
の極限を考えてみよう。
今、上のように、
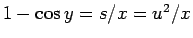 とすると、
とすると、
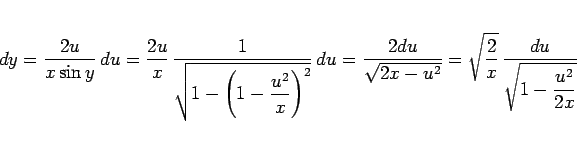
となるから、(18) は
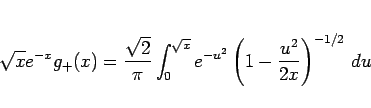 |
(19) |
となる。 のとき
のとき
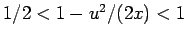 に注意すると、
(19) より
に注意すると、
(19) より
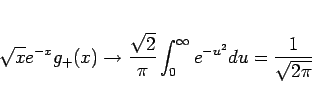
が言えるので、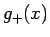 の第 1 近似は
の第 1 近似は
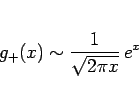
となる。
第 2 近似は、
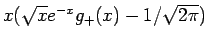 の極限を考える。
(19) より、
の極限を考える。
(19) より、
![\begin{eqnarray*}\lefteqn{x\left(\sqrt{x}e^{-x}g_{+}(x)-\frac{1}{\sqrt{2\pi}}\ri...
...ht)^{-1/2}-1\right\}du
-\int_{\sqrt{x}}^\infty e^{-u^2}du\right]\end{eqnarray*}](img176.gif)
と変形すると、
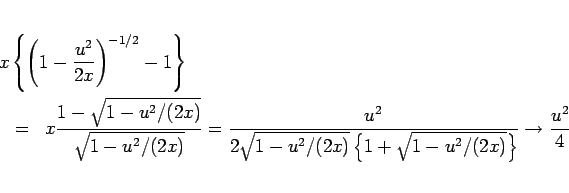
となる。また
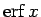 の漸近展開式 (5) より、
の漸近展開式 (5) より、
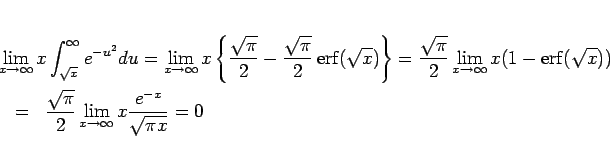
であるから、
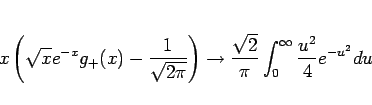
となることがわかる。
これは、より形式的に次のようにしても得られる。
一般二項定理
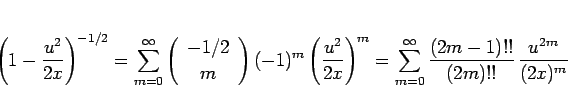
より、(19) から
であるから、
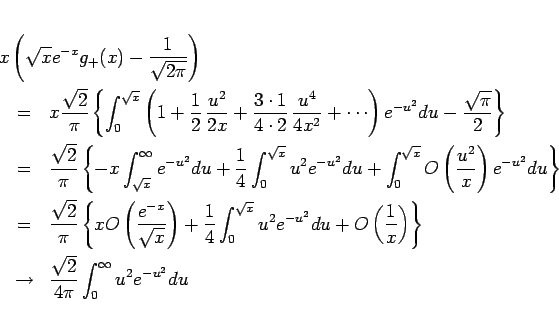
となる。
そしてこの計算を繰り返すことにより、
実は (20) の右辺の
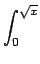 を
を
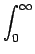 にしたものが (20) の
左辺の漸近展開であることがわかる。
にしたものが (20) の
左辺の漸近展開であることがわかる。
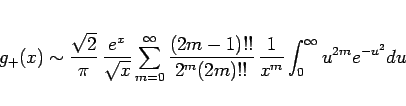 |
(21) |
後はこの最後の積分を求めればよい。今、
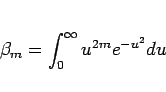
とすると、部分積分により、
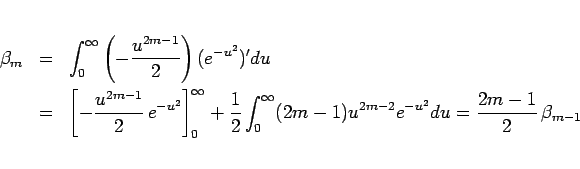
となるので、
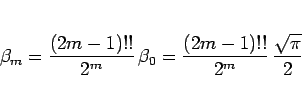
となり、結局 (21) は
のようになる。
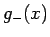 の漸近展開 (17) と
の漸近展開 (17) と 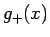 の漸近展開 (22) を比較すると、
明らかに (22) の各項は (17) の
すべての項より大きいので、
結局 (22) が
の漸近展開 (22) を比較すると、
明らかに (22) の各項は (17) の
すべての項より大きいので、
結局 (22) が 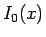 の漸近展開であることがわかる。
の漸近展開であることがわかる。
竹野茂治@新潟工科大学
2010年4月8日
![]() を考えよう。
を考えよう。![]() では
では ![]() だから、
だから、
![]() のとき、
のとき、
![]() の 1 への収束は、
の 1 への収束は、![]() が 0 に近い程遅くなる。
つまりその近くが最も大きな項を与えると予想される。
よって
が 0 に近い程遅くなる。
つまりその近くが最も大きな項を与えると予想される。
よって ![]() をさらに 2 つに分け、
をさらに 2 つに分け、
![]() では、
では、![]() であるから、
であるから、
![]() の方は、
の方は、![]() とすると、
とすると、
![]() の最も大きい項は
の最も大きい項は ![]() の
の ![]() の項
だろうと予想される。
実際、部分積分により、
の項
だろうと予想される。
実際、部分積分により、
![]() とすると、
再び部分積分により、
とすると、
再び部分積分により、
![]() の主要項である
の主要項である ![]() の方を考える。
の方を考える。
![]() は、
は、
![]() のときに明らかに無限大に発散するが、
のときに明らかに無限大に発散するが、
![]() とすると、
とすると、
![]() であるから、
であるから、
![]() とすると、
とすると、
![]() の極限を考える。
(19) より、
の極限を考える。
(19) より、
![]() を
を
![]() にしたものが (20) の
左辺の漸近展開であることがわかる。
にしたものが (20) の
左辺の漸近展開であることがわかる。
![]() の漸近展開 (17) と
の漸近展開 (17) と ![]() の漸近展開 (22) を比較すると、
明らかに (22) の各項は (17) の
すべての項より大きいので、
結局 (22) が
の漸近展開 (22) を比較すると、
明らかに (22) の各項は (17) の
すべての項より大きいので、
結局 (22) が ![]() の漸近展開であることがわかる。
の漸近展開であることがわかる。