6 公転による変化

まず、地球と太陽の距離 $\rho$ と地球の半径 r は、理科年表 [1] によれば $\rho$ $\approx$ 2.35 x 10⁴r くらいであり、 $\rho$ $\gg$ r なので、 r の項を無視して考え、その場合の太陽の位置を $\bar{{\mathrm{O}}}$ 、回転の中心を $\bar{{\mathrm{S}}}$ と書くことにすると、

$\bar{{\mathrm{S}}}$ は、P を通り $\mu$ に平行な直線上にあり、この直線は太陽の軌道面とは垂直になり、 $\bar{{e}}_{y}^{}$ とは角度 $\theta$ をなす。この $\bar{{\mathrm{S}}}$ の位置は、公転によって変化する sin $\beta$ の値とともにこの直線上を移動し、例えば北半球 ( 0 < $\theta$ < $\pi$ /2 ) では、 $\mu$ は斜め上向きのベクトルになるから、 sin $\beta$ < 0 のときにその中心は地表平面より上に、 sin $\beta$ > 0 のときには地表平面より下にあり、 sin $\beta$ = 0 のときに P に一致する。つまり、 sin $\beta$ < 0 の季節は昼の方が長く、 sin $\beta$ > 0 の季節は夜の方が長く、 sin $\beta$ = 0 のときが春分、秋分、ということになる。よってこの春分、秋分は緯度 $\theta$ にはよらず、 $\beta$ のみで決定することがわかる。

一方太陽の軌道は、 $\bar{{e}}_{x}^{}$ と $\xi$ を通る平面に平行な面上での円軌道であり、すなわち回転軸が $\mu$ であるので、これは緯度 $\theta$ の分だけ傾いた軌道を描く (図 7)。太陽軌道面の傾きは季節 $\beta$ には関係なく、緯度によって決定する。

**図 7:** 太陽の軌道 (点線は各軌道の地表平面の高さ)
$\includegraphics[height=0.2\textheight]{orbit1.eps}$

図 7 でいうと、軌道 o_a は地表に出ている部分が短く (冬)、 o_c は地表に出ている部分が長い (夏)。 o_b が春分、秋分のときを表している。この春分、秋分のときは、太陽は真東から登り、真西に沈み、最も高い方向は $\xi$ の方向に等しくなる。円軌道面はそれぞれが平行なのであるが、 P から観測すると冬の太陽は小さい仰角、夏の太陽は大きい仰角のところにあがることになる。

緯度による変化を考えると、高緯度地域、例えば北極に向えば $\theta$ が $\pi$ /2 に近づくので、 $\mu$ は $\bar{{e}}_{z}^{}$ に近づく。よって太陽軌道面は水平面 (地表平面) に近づくので太陽は上には上がらず、横に転がるような運動となる。その軌道面は季節によって上下に移動するので、その転がる軌道面が 1 日中地表平面の上に出ている季節が「白夜」となる¹。

逆に赤道では、 $\theta$ = 0 であるから $\mu$ = $\bar{{e}}_{y}^{}$ 、 $\xi$ = $\bar{{e}}_{z}^{}$ となり、軌道面は傾かずに $\bar{{e}}_{x}^{}$ , $\bar{{e}}_{z}^{}$ に平行な面となる。この場合は、中心 $\bar{{\mathrm{S}}}$ は、常に $\bar{{e}}_{y}^{}$ 軸上にあるので、春分に限らず毎日昼と夜の長さが等しいことになる。つまり赤道では、春分、秋分は「昼と夜の長さが等しい」日ではなく、むしろ「太陽が真東から登り、真上で最高点に達し、真西に沈む日」ということになる。逆に春分、秋分以外では太陽は真上までは登らないので、赤道ではこの春分、秋分の時期が最も暑い真夏、ということになりそうである。

実は太陽の軌道の半径 R = 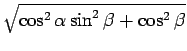$\rho$ $\sqrt{{\cos^2\alpha\sin^2\beta+\cos^2\beta}}$ も季節 $\beta$ によって変化する。

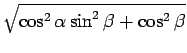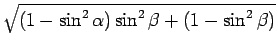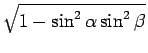R	=	$\displaystyle \rho$ $\displaystyle \sqrt{{\cos^2\alpha\sin^2\beta+\cos^2\beta}}$ = $\displaystyle \rho$ $\displaystyle \sqrt{{(1-\sin^2\alpha)\sin^2\beta+(1-\sin^2\beta)}}$
	=	$\displaystyle \rho$ $\displaystyle \sqrt{{1-\sin^2\alpha\sin^2\beta}}$