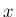
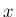 の
値の集合
の
値の集合 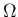 は通常実数全体 Rで、
その確率は、
は通常実数全体 Rで、
その確率は、
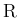 の部分集合
の部分集合
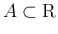 に対して、
に対して、
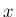 の値が
の値が 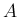 に含まれる確率
に含まれる確率
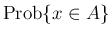 を考え、
1 点の値に対する確率
を考え、
1 点の値に対する確率
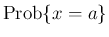 は 0 とする。
は 0 とする。
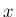 の確率分布は、分布関数
の確率分布は、分布関数 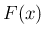 、
またはその導関数である密度関数
、
またはその導関数である密度関数 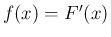 によって決定する。
分布関数 (累積分布関数)
によって決定する。
分布関数 (累積分布関数) 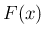 は、
と定義され、1 点の確率が 0 であれば非減少な連続関数となる。
は、
と定義され、1 点の確率が 0 であれば非減少な連続関数となる。
(12) により 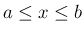 となる確率は
となる確率は
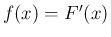 は、(13) より、
となり、さらに一般に
は、(13) より、
となり、さらに一般に
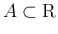 に対して
となる。
に対して
となる。
分布関数 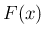 は、
は、
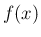 は、
を満たす必要がある。
は、
を満たす必要がある。
逆に、(16) を満たす 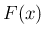 を取れば、
を取れば、
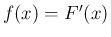 により密度関数が定まり、
それにより (15) で
により密度関数が定まり、
それにより (15) で 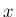 の確率が求まるので、
これで一つの連続確率分布が決定する。
の確率が求まるので、
これで一つの連続確率分布が決定する。
または、(17) を満たす 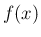 を取れば、
(15) から
を取れば、
(15) から 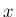 の確率が求まるので、
一つの連続確率分布が決定し、その分布関数
の確率が求まるので、
一つの連続確率分布が決定し、その分布関数 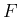 も
も
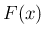 、
密度関数
、
密度関数 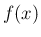 のいずれかを設定すればよいので、
とりあえず本稿では
のいずれかを設定すればよいので、
とりあえず本稿では
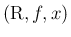 の組を「連続確率分布」と呼ぶことにする。
の組を「連続確率分布」と呼ぶことにする。
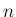 個の連続確率分布
個の連続確率分布
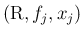 (
(
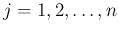 ) において、
Rの部分集合
) において、
Rの部分集合
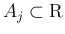 (
(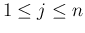 ) に対して、
) に対して、
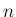 次元連続確率分布を構成できる。
なお、
次元連続確率分布を構成できる。
なお、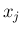 の分布関数を
の分布関数を 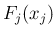 とする。
とする。
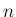 次元確率変数
次元確率変数
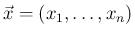 の
分布関数
の
分布関数 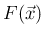 を、
を、
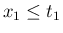 かつ ...
かつ ...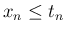 となる確率に
よって定義する。
となる確率に
よって定義する。
このとき、
![\begin{eqnarray*}\lefteqn{\mathrm{Prob}\{\vec{x}\in (a_1,b_1]\times(-\infty,t_2]...
...1\int_{a_2}^{b_2}dt_2\int_{a_3}^{b_3}
F_{x_1x_2x_3}(\vec{t})dt_3\end{eqnarray*}](img84.png)
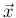 の密度関数
の密度関数 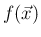 を
この分布関数の
を
この分布関数の 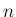 階導関数
と定義すれば、
となり、より一般に
階導関数
と定義すれば、
となり、より一般に
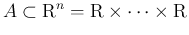 に対して
となる。
に対して
となる。
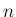 次元分布関数
次元分布関数 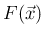 は、
は、
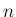 次元密度関数
次元密度関数 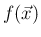 は
を満たす。
は
を満たす。
さらに周辺分布として、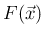 は
は 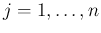 に対して
に対して
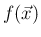 は
は 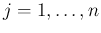 に対して
を満たす。この (28) は、
この左辺を
に対して
を満たす。この (28) は、
この左辺を 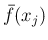 とすると、(23) より
とすると、(23) より
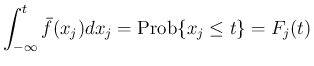
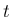 で微分すれば
で微分すれば
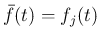 となること
から得られる。
となること
から得られる。
逆に (25) を満たす 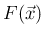 によって (22) と (24) から
一つの
によって (22) と (24) から
一つの 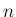 次元連続確率分布が決定し、(27) に
よって周辺分布が決定する。
次元連続確率分布が決定し、(27) に
よって周辺分布が決定する。
そしてそれらは 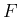 の代わりに (26) を
満たす
の代わりに (26) を
満たす 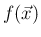 によっても決定する。
この
によっても決定する。
この 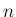 次元連続確率分布を
次元連続確率分布を
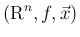 と書くことにする。
と書くことにする。
竹野茂治@新潟工科大学