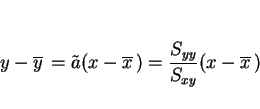

Next: 5 点と直線の距離を用いた回帰直線
Up: 相関係数に関する一考察
Previous: 3 通常の回帰直線の定義
(PDF ファイル: corel1.pdf)
4 回転不変性について
これまでにあげた疑問を考えていくが、
まずは問題 2 としてあげた
相関係数や回帰直線の回転不変性について考える。
データ 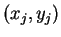 を、原点の周りに
を、原点の周りに 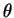 回転したデータを
回転したデータを
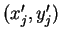 とする。すなわち
とする。すなわち
とすれば、
なので、
となる。この式から、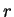 が
が 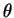 に関して不変でないことはすぐに分かる。
に関して不変でないことはすぐに分かる。
しかし、回転不変な式もいくつか容易に見つかる。例えば
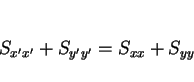 |
(2) |
であるし、また、
より、
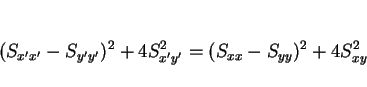 |
(3) |
のような不変量も得られるし、これら 2 つを組み合わせて
(
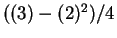 )、
)、
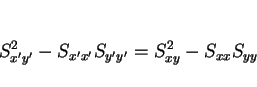 |
(4) |
のような不変量も得られる。
また、この回転されたデータに対する回帰直線は
であり、これは
とパラメータ表示される。よって、この両辺に 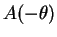 をかけて
この直線を原点の周りに
をかけて
この直線を原点の周りに 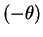 回転すると
回転すると
となる。ここで、
となるので、この直線の傾き 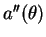 は
は
となる。
これは 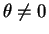 であればもちろん通常の回帰直線の傾き
であればもちろん通常の回帰直線の傾き
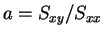 とは一致しない。
つまり、回帰直線も回転不変性を持たないことがわかる。
とは一致しない。
つまり、回帰直線も回転不変性を持たないことがわかる。
なお、この 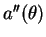 の、
の、
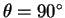 のときの値は、
のときの値は、
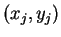 を
を 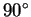 回したデータに対する回帰直線を
回したデータに対する回帰直線を 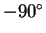 回した直線の傾き
回した直線の傾き
を意味するが、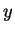 軸に関して折り返して考えれば容易に分かるが、
その傾きは、3 節でも言及した、
軸に関して折り返して考えれば容易に分かるが、
その傾きは、3 節でも言及した、
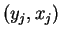 に対する回帰直線を、
に対する回帰直線を、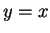 に関して対称に折り返したものの傾き
に関して対称に折り返したものの傾き
に等しい。つまり、そのような直線を表す式は
であることがわかる。この直線も元の回帰直線とは一致しない。


Next: 5 点と直線の距離を用いた回帰直線
Up: 相関係数に関する一考察
Previous: 3 通常の回帰直線の定義
Shigeharu TAKENO
2004年 10月 18日
![]() を、原点の周りに
を、原点の周りに ![]() 回転したデータを
回転したデータを
![]() とする。すなわち
とする。すなわち
![\begin{displaymath}
\left[\begin{array}{c}x'_j\\ y'_j\end{array}\right] = A(\the...
...\theta &-\sin\theta\\ \sin\theta &\cos\theta\end{array}\right]
\end{displaymath}](img69.gif)
![\begin{displaymath}
\left[\begin{array}{c}\overline{x'}\,\\ \overline{y'}\,\end{...
...y}{c}x_j-\overline{x}\,\\ y_j-\overline{y}\,\end{array}\right]
\end{displaymath}](img70.gif)
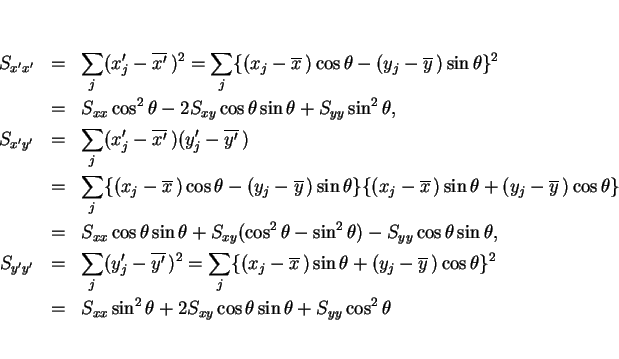
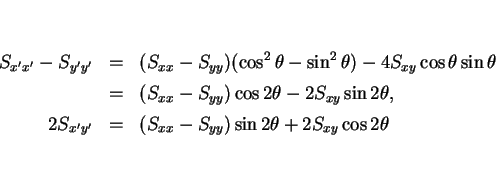
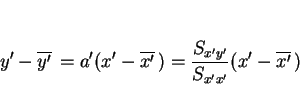
![\begin{displaymath}
\left[\begin{array}{c}x'-\overline{x'}\,\\ y'-\overline{y'}\...
...array}\right]
=t\left[\begin{array}{c}1\\ a'\end{array}\right]
\end{displaymath}](img78.gif)
![\begin{eqnarray*}&& A(-\theta)\left[\begin{array}{c}x'-\overline{x'}\,\\ y'-\ove...
...a\\
-S_{x'x'}\sin\theta+S_{x'y'}\cos\theta\end{array}\right]\\ \end{eqnarray*}](img81.gif)
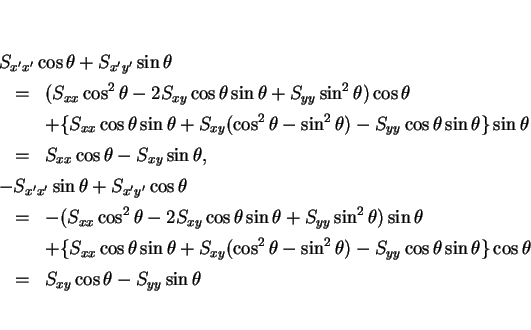
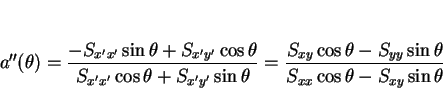
![]() の、
の、
![]() のときの値は、
のときの値は、
を
回したデータに対する回帰直線を
回した直線の傾き
に対する回帰直線を、
に関して対称に折り返したものの傾き