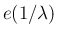
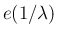 の裏が
ポアソン分布
の裏が
ポアソン分布 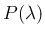 となることを考える。
となることを考える。
4 節と同様に、最後にその事象が起きたところを時刻 0 として
考える。
時刻 0 から 1 回目の事象が起こるまでの時間を 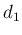 、
、
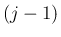 回目の事象から
回目の事象から 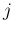 回目の事象までの
時間を
回目の事象までの
時間を 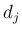 とする (
とする (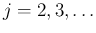 )。
)。
このとき、例えば 1 時間以内に 2 回の事象が収まる
確率
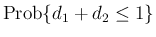 は、
1 時間以内に起こる回数
は、
1 時間以内に起こる回数 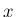 で見ると
で見ると
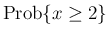 に対応する (
に対応する (
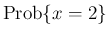 ではない)。よって、一般に、
ではない)。よって、一般に、
この左辺は、前節例 7 より独立な指数分布の和である
ガンマ分布
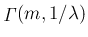 に従うので、
その密度関数
に従うので、
その密度関数
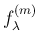 の 1 までの積分で表される。
の 1 までの積分で表される。
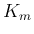 と書くことにする (
と書くことにする (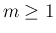 )。同様にして、
)。同様にして、
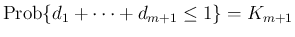
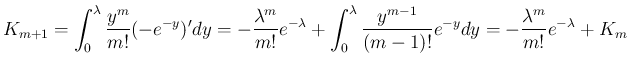
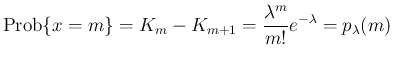
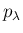 の形になる (
の形になる (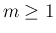 )。
)。
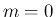 のときは、(7) で
のときは、(7) で 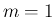 として 1 から引けば、
として 1 から引けば、
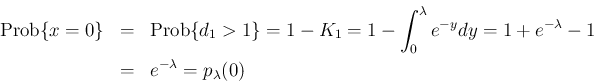
よって、指数分布 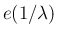 を時間間隔とする独立な事象の 1 時間の
回数の分布はポアソン分布
を時間間隔とする独立な事象の 1 時間の
回数の分布はポアソン分布 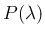 であることが示された。
であることが示された。
竹野茂治@新潟工科大学