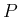
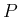 を、標本空間
を、標本空間 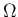 と、
その上の確率関数
と、
その上の確率関数
![$p(x):\Omega\rightarrow [0,1]$](img3.png) をセットにして、
をセットにして、
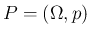 のように表す。
なお、
のように表す。
なお、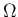 としては、基本的に
としては、基本的に
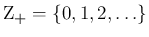 を考える。
を考える。
離散確率分布
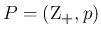 ,
,
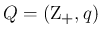 のたたみこみを紹介する。
確率変数
のたたみこみを紹介する。
確率変数 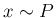 ,
, 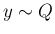 が独立であるとみて、その和
が独立であるとみて、その和 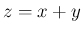 を考える。
独立なので、2 次元確率関数
を考える。
独立なので、2 次元確率関数 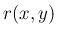 は
は
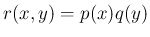 となり、
その写像
となり、
その写像
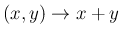 として
として 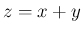 が定まるが ([1])、
この
が定まるが ([1])、
この 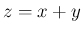 の確率関数
の確率関数 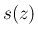 は、
は、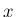 と
と 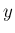 の独立性より、
の独立性より、
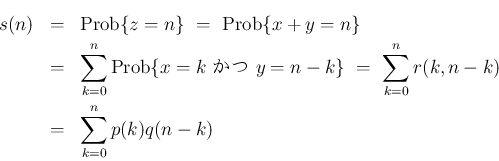
このように、2 つの確率分布
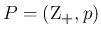 ,
,
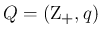 に対して、
に対して、
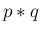 を確率関数とする確率分布を
を確率関数とする確率分布を 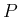 ,
, 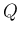 の
「たたみこみ」といい、
の
「たたみこみ」といい、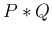 と書く。
なお、
と書く。
なお、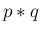 の値は当然 0 以上であり、
の値は当然 0 以上であり、
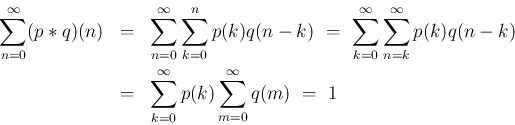
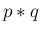 は Z
は Z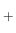 上の確率関数となる。
たたみこみ
上の確率関数となる。
たたみこみ 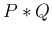 は、上に見たように
は、上に見たように 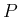 ,
, 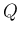 に従う
独立な確率変数の和が従う確率分布、となる。
に従う
独立な確率変数の和が従う確率分布、となる。
たたみこみに関しては、以下が成り立つ。
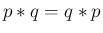
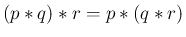
 上の確率関数
上の確率関数 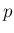 ,
, 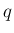 に対して、
に対して、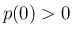 のとき、
のとき、
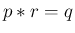 となる Z
となる Z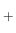 上の関数
上の関数 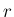 が一意に決定する (が、確率関数になるとは限らない)
が一意に決定する (が、確率関数になるとは限らない)
証明
1. 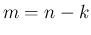 とすると、
とすると、
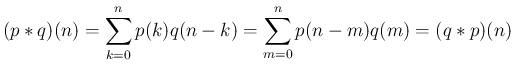
2.
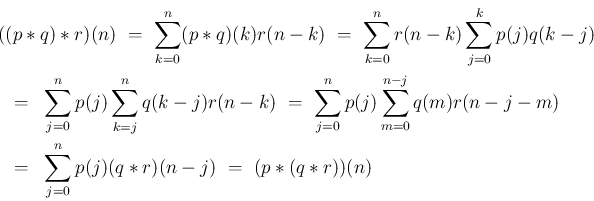
3. 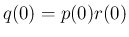 なので、
なので、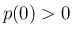 より
より 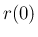 は
は
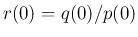 と
一意に決定する。
と
一意に決定する。
また、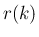 が
が
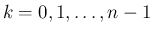 まで決定したとすると、
まで決定したとすると、
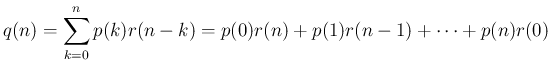
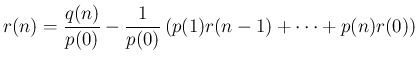
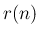 も一意に決定するから、
も一意に決定するから、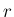 が一意に決定することになる。
が一意に決定することになる。
ただし、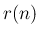 の値が負にならないとは言えないので、
の値が負にならないとは言えないので、
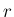 が確率関数になるとは限らない。
が確率関数になるとは限らない。
この命題 1 の 2. より、
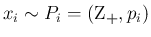 (
(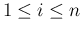 ) に対するたたみこみ
) に対するたたみこみ
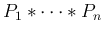 を考えることもできる。
これは、順にたたみこんだものであるが、
を考えることもできる。
これは、順にたたみこんだものであるが、
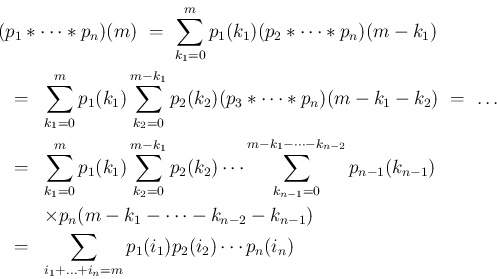
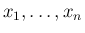 が独立であるとみたときの
が独立であるとみたときの
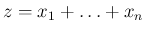 が
が 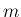 に等しい確率になるので、
に等しい確率になるので、
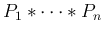 はこの和の確率分布となる。
はこの和の確率分布となる。
また、この 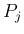 がすべて
がすべて
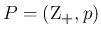 に等しい場合は、
それを本稿では
に等しい場合は、
それを本稿では
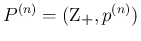 と書くことにする。
命題 1 の 3. と同様、これに対しても
次が成り立つ。
と書くことにする。
命題 1 の 3. と同様、これに対しても
次が成り立つ。
Z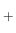 上の確率関数
上の確率関数 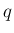 と
と 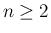 に対して、
に対して、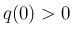 のとき、
のとき、
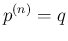 となる Z
となる Z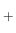 上の関数
上の関数 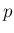 が一意に決定する (が、確率関数になるとは限らない)
が一意に決定する (が、確率関数になるとは限らない)
証明
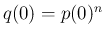 より、
より、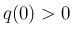 であれば
であれば
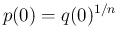 と
一意に
と
一意に 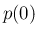 が決定する。
が決定する。
また、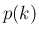 が
が
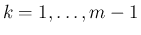 まで決定したとすると、
まで決定したとすると、
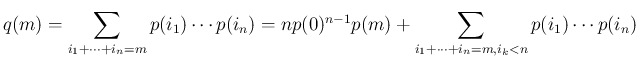
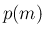 は、
は、
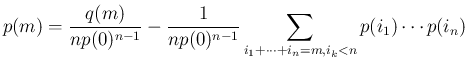
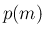 が一意に決定する。
が一意に決定する。
ただし、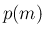 の値が負にならないとは言えないので、
の値が負にならないとは言えないので、
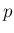 が確率関数になるとは限らない。
が確率関数になるとは限らない。
ここで、たたみこみの例を 2,3 紹介する。
2 項分布
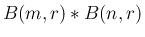 のたたみこみを計算する。
2 項分布
のたたみこみを計算する。
2 項分布 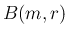 の確率関数を
の確率関数を
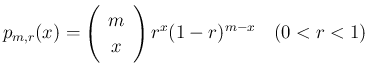
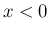 , または
, または 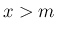 では
では
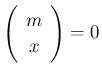
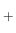 とする。
とする。
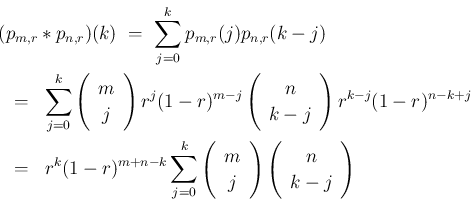
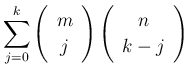
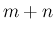 個の玉のうち、
個の玉のうち、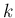 個が白玉、
個が白玉、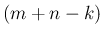 個が赤玉であるときに
それを 1 列に並べたときの並べかえの個数
個が赤玉であるときに
それを 1 列に並べたときの並べかえの個数
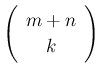
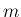 個と後の
個と後の 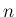 個に分けて
考えると、その並び換えの総数は、最初の
個に分けて
考えると、その並び換えの総数は、最初の 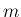 個に
個に 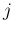 個の白玉が含まれ、
後の
個の白玉が含まれ、
後の 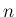 個に
個に 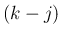 個の白玉が含まれるときの組み合わせの総数を、
個の白玉が含まれるときの組み合わせの総数を、
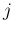 に関して加えたものになっているからである。
に関して加えたものになっているからである。
よって、
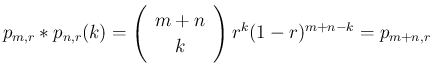
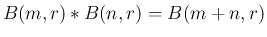 となることがわかる。
一般に、
となることがわかる。
一般に、
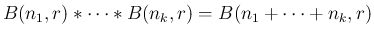
ポアソン分布
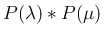 のたたみこみを計算する。
ポアソン分布
のたたみこみを計算する。
ポアソン分布 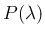 の確率関数を
の確率関数を
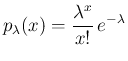
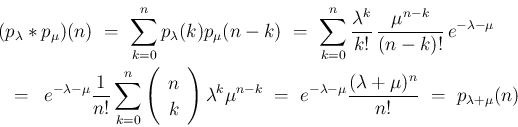
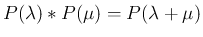 がわかる。
一般に、
がわかる。
一般に、
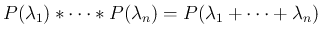
竹野茂治@新潟工科大学