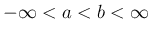
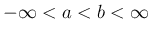 とする。
とする。
 が
が  上の関数で、
上の関数で、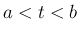 なる任意の
なる任意の 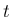 に対して
に対して ![$[a,t]$](img32.png) 上
上 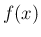 は有界でかつ積分可能で、
は有界でかつ積分可能で、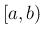 では有界ではない場合、
では有界ではない場合、
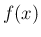 が
が ![$(a,b]$](img34.png) 上の関数で、
上の関数で、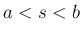 なる任意の
なる任意の 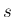 に対して
に対して ![$[s,b]$](img37.png) 上
上 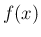 は有界でかつ積分可能で、
は有界でかつ積分可能で、![$(a,b]$](img34.png) では有界ではない場合、
では有界ではない場合、
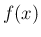 が
が 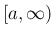 上の関数で、
上の関数で、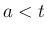 なる任意の
なる任意の 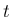 に対して
に対して ![$[a,t]$](img32.png) 上
上 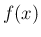 は有界でかつ積分可能である場合、
は有界でかつ積分可能である場合、
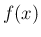 が
が ![$(-\infty,b]$](img42.png) 上の関数で、
上の関数で、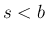 なる任意の
なる任意の 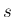 に対して
に対して ![$[s,b]$](img37.png) 上
上 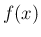 は有界でかつ積分可能である場合、
は有界でかつ積分可能である場合、
上記の広義積分は、いずれも積分範囲の片端で通常の積分が できない場合であるが、 積分範囲の両端で積分ができない「合併型」もある。 その場合は、2 重極限で考えればよい。
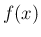 が
が 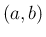 上の関数で、
上の関数で、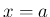 ,
, 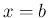 の近くで有界ではない場合、
の近くで有界ではない場合、
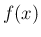 が
が 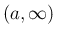 上の関数で、
上の関数で、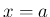 の近くで有界ではない場合、
の近くで有界ではない場合、
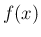 が
が 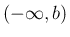 上の関数で、
上の関数で、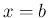 の近くで有界ではない場合、
の近くで有界ではない場合、
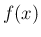 が
が
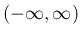 上の関数である場合、
上の関数である場合、
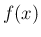 は
は 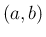 上の関数で、
上の関数で、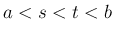 となる任意の
となる任意の 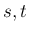 に対し、
に対し、
![$[s,t]$](img57.png) 上
上 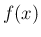 は有界かつ積分可能で、
は有界かつ積分可能で、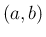 では有界ではないとする。
では有界ではないとする。
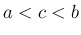 となる
となる 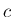 をひとつ取って考え、
をひとつ取って考え、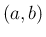 での
での 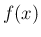 の
原始関数のひとつを
の
原始関数のひとつを 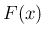 とする。例えば、
とする。例えば、
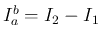 となる。
となる。
逆に、(15) の有限な極限値が存在する場合、
これは 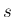 ,
, 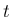 に関する独立な極限なので、
(16) の極限が両方とも存在する必要がある。
つまり、(10) が存在するかどうかは、
(16) の両方が存在するかどうかに
一致することになる。
さらにこの場合、
に関する独立な極限なので、
(16) の極限が両方とも存在する必要がある。
つまり、(10) が存在するかどうかは、
(16) の両方が存在するかどうかに
一致することになる。
さらにこの場合、
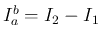 は、(14) により、
は、(14) により、
つまり、(10) の 2 重極限による定義を、
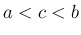 なるひとつの
なるひとつの 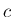 に対して、
(17) の両方の広義積分が有限値で存在するときに (17) によって定義する、としても同じことになる。
実際 (10) の広義積分をそのように定義している本も多い。
に対して、
(17) の両方の広義積分が有限値で存在するときに (17) によって定義する、としても同じことになる。
実際 (10) の広義積分をそのように定義している本も多い。
なお、この 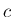 は
は 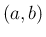 内であればなんでもよく、
ひとつの
内であればなんでもよく、
ひとつの 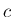 に対して広義積分が存在すれば
他の
に対して広義積分が存在すれば
他の 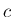 に対しても当然積分は存在して同じ値になるし、
ひとつの
に対しても当然積分は存在して同じ値になるし、
ひとつの 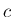 に対して存在しなければ、他の
に対して存在しなければ、他の 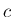 に対しても存在しない。
に対しても存在しない。
これは、(11), (12), (13) についても同様であり、
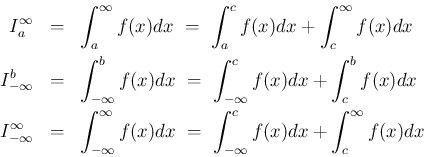
ただし、注意しなければいけないのは、 (10) の 2 重極限を、簡単にひとつにまとめて、
とやってはいけないことである。 2 つの極限の近づき方が独立でないと (10) とは違うものになる。 (10) が存在すれば、(18) も存在して、 確かに両者は同じ値になるが、逆は必ずしもそうではなく、 すなわち (18) は有限値で存在しても、 (10) が存在しない例が作れる。 例えば、![$[0,2]$](img72.png) の関数
の関数 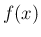 を
とすると、
を
とすると、
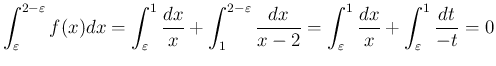
![$\displaystyle \int_\varepsilon^1 f(x) dx
=\int_\varepsilon^1\frac{dx}{x}
=[\log x]_\varepsilon^1
= -\log\varepsilon
\rightarrow\infty
$](img75.png)
![$(0,1]$](img76.png) の広義積分は存在しないし、
同様に
の広義積分は存在しないし、
同様に 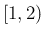 の広義積分も存在しない。
よって、この
の広義積分も存在しない。
よって、この 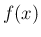 に対して (10) は存在しない。
に対して (10) は存在しない。
なお、(10) が存在せず (18) が 存在する場合、(18) を (10) の 「主値」や「有限部分」などと呼ぶ場合がある。
また、もうひとつの合併型として、積分区間 ![$[a,b]$](img3.png) の内部
の内部 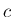 (
(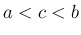 ) で
有界でない場合も考えられるが、その場合は
) で
有界でない場合も考えられるが、その場合は
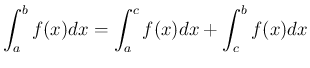
合併型の広義積分の具体例としては、ベータ関数
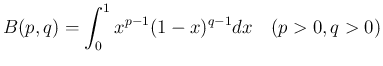
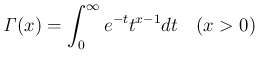
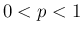 ,
, 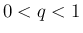 のときに
のときに 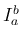 型の広義積分、
ガンマ関数は
型の広義積分、
ガンマ関数は 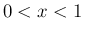 のときに
のときに 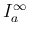 型の広義積分となる。
型の広義積分となる。
竹野茂治@新潟工科大学