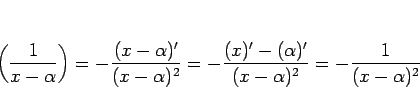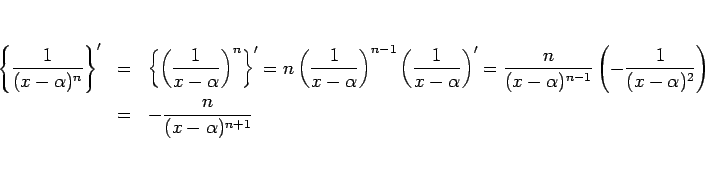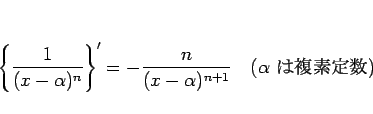 |
(16) |
まず、複素数が含まれている実数変数の関数の微分と積分の意味について 定義しておく。
複素数値関数
![]() (
(![]() は実数、
は実数、![]() ,
, ![]() は実数値関数)
に対して、その微分と積分を次のように定義する。
は実数値関数)
に対して、その微分と積分を次のように定義する。
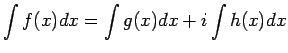
![]() は定数 (
は定数 (![]() ) であることを考えれば、これは自然な定義である。
これに対し、次が成り立つ。
) であることを考えれば、これは自然な定義である。
これに対し、次が成り立つ。
複素数値関数 ![]() ,
, ![]() に対し、次が成り立つ。
に対し、次が成り立つ。
証明
以下、![]() ,
, ![]() を実数部分、虚数部分に分けて、
を実数部分、虚数部分に分けて、
![]() ,
, ![]() とする。
とする。
1.
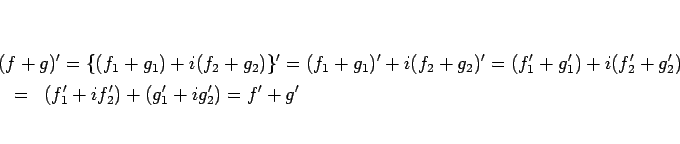
2.
![]() (
(![]() は実数) とすると、
は実数) とすると、
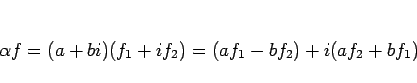
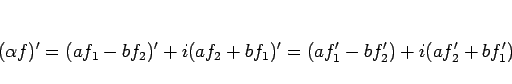
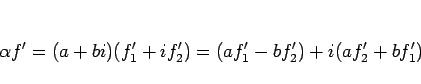
3.
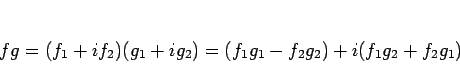
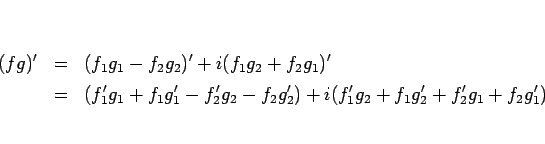
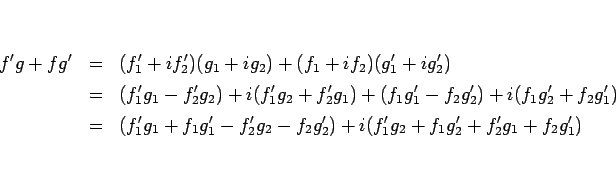
4.
まず、
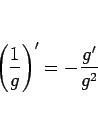
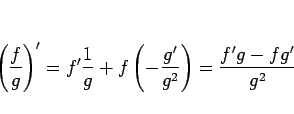
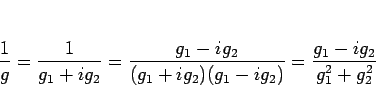
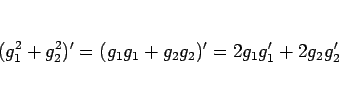
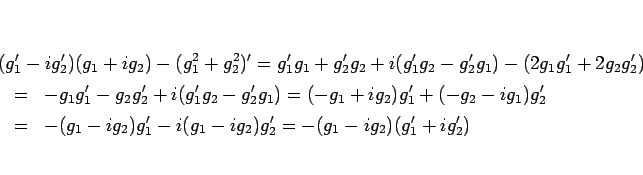
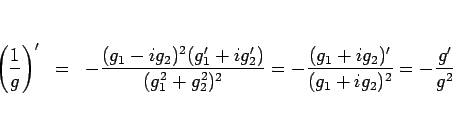
5. これは、積の微分 3. を繰り返し用いれば (または、厳密に示すならば帰納法で) 得られる。
(16) の証明