次へ: 3 偶数次、奇数次による対称性
上へ: 複素数を利用した有理関数の積分
前へ: 1 はじめに
(PDF ファイル: quotef4.pdf)
2 共役による対称性
分子が奇数次の場合は容易に積分できるので、
ここでは分子が偶数次の場合にのみ限定し、
を考えることにする。
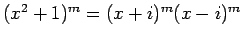 なので
[3] で述べたように、
なので
[3] で述べたように、
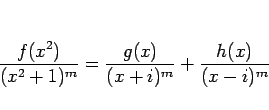 |
(1) |
のように部分分数分解できる。
ここで、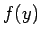 は
は 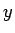 に関する実数係数の
に関する実数係数の 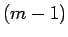 次の整式とし、
次の整式とし、
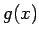 ,
, 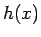 は複素数係数の高々
は複素数係数の高々 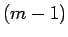 次の整式になる。
次の整式になる。
分母を払えば、
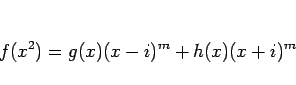 |
(2) |
となるが、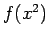 は実数係数なのでこの両辺の共役を取ると、
は実数係数なのでこの両辺の共役を取ると、
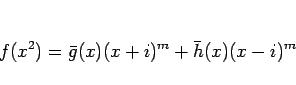 |
(3) |
となる。ここで、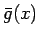 は、
は、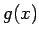 の係数を
すべて共役複素数にした整式を意味する。
(2), (3) により、
の係数を
すべて共役複素数にした整式を意味する。
(2), (3) により、
よって、
が成り立つ。
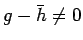 であれば
左辺の因子である
であれば
左辺の因子である 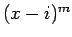 は右辺の因子にもなるが、
それは
は右辺の因子にもなるが、
それは 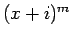 とは互いに素なので、
とは互いに素なので、
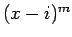 は
は 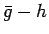 の因子であるはずである。
しかし、
の因子であるはずである。
しかし、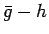 の次数
の次数
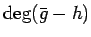 は
は
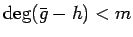 であるから、
これは
であるから、
これは 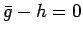 を意味し、それは
を意味し、それは
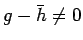 に反する。
よって背理法により
に反する。
よって背理法により
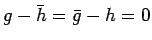 となるので、
(1) は、
となるので、
(1) は、
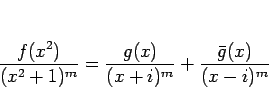 |
(4) |
という形になる。
(1) だと、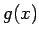 ,
, 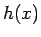 の自由度があるが、
(4) だと
の自由度があるが、
(4) だと 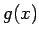 だけの自由度なので
未定係数法で考える場合多少楽になる。
だけの自由度なので
未定係数法で考える場合多少楽になる。
しかし、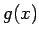 が高々
が高々 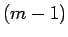 次式だとは言ってもその係数は複素数なので、
係数は複素数
次式だとは言ってもその係数は複素数なので、
係数は複素数 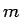 個、すなわち実数
個、すなわち実数 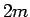 個の自由度がまだあることになる。
個の自由度がまだあることになる。
次へ: 3 偶数次、奇数次による対称性
上へ: 複素数を利用した有理関数の積分
前へ: 1 はじめに
竹野茂治@新潟工科大学
2006年6月2日
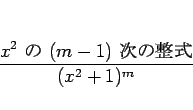
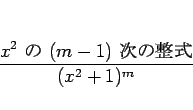
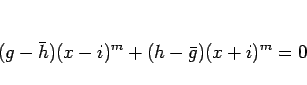
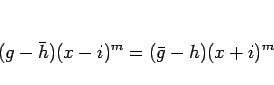
![]() が高々
が高々 ![]() 次式だとは言ってもその係数は複素数なので、
係数は複素数
次式だとは言ってもその係数は複素数なので、
係数は複素数 ![]() 個、すなわち実数
個、すなわち実数 ![]() 個の自由度がまだあることになる。
個の自由度がまだあることになる。