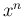
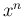 と
と 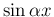 ,
, 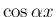 の積の積分を考える。
の積の積分を考える。
これも、大まかな方針は、部分積分を繰り返して、 巾乗の方の次数を一つずつ下げることで、 最終的に三角関数のみの積分に帰着させることである。
一般的な式を求める方法はいくつか考えられるが、 例えば以下のようなものがある。
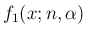 のような関数を見つけて、
積の微分により求める
のような関数を見つけて、
積の微分により求める
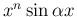 ,
,
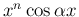 の部分積分は、
毎回の部分積分で、
の部分積分は、
毎回の部分積分で、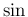 と
と 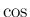 が交互に入れ替わるので、
1. の方針では 2 節ほど簡単ではない。
本節ではまずそれを考えてみる。
が交互に入れ替わるので、
1. の方針では 2 節ほど簡単ではない。
本節ではまずそれを考えてみる。
とすると、これも当然 となって
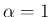 の場合に帰着される。
部分積分により、
の場合に帰着される。
部分積分により、
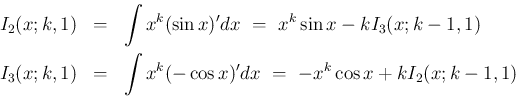
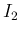 と
と 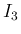 が混在するので 2 節
よりはだいぶ厄介になる。
その回避策としては、例えばもう 1 段下げて
が混在するので 2 節
よりはだいぶ厄介になる。
その回避策としては、例えばもう 1 段下げて 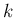 と
と 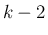 の関係式にする、
という手がある。
の関係式にする、
という手がある。
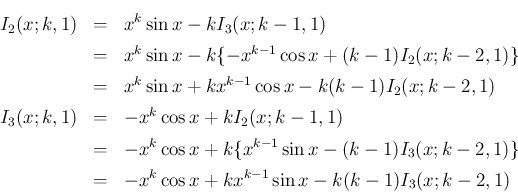
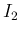 と
と 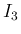 が混在しない
漸化式が得られるので、あとは
が混在しない
漸化式が得られるので、あとは
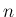 が奇数か偶数かで場合分けすれば
が奇数か偶数かで場合分けすれば 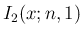 ,
, 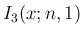 の
一般的な式を得ることができる。
ただし、その場合分けも含めて、
その一般的な式は 2 節のものよりはだいぶ複雑に
なる (が、これも不思議と
の
一般的な式を得ることができる。
ただし、その場合分けも含めて、
その一般的な式は 2 節のものよりはだいぶ複雑に
なる (が、これも不思議と 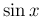 ,
, 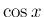 のマクローリン展開に
似た形になる)。
のマクローリン展開に
似た形になる)。
それを解消する方法として、さらに次のような手がある。
とすると、これは、 となるので、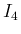 は
は 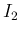 ,
, 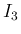 を特別な場合として含んでいて、
つまり
を特別な場合として含んでいて、
つまり 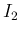 ,
, 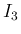 を一般化したものとも見ることができる。
を一般化したものとも見ることができる。
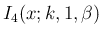 を部分積分すると、
を部分積分すると、
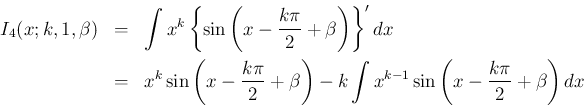
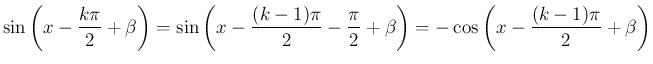
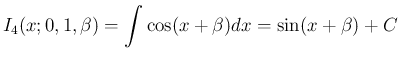
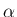 の場合も、
の場合も、
例えば、これを簡単なものに適用すると、(17), (19) より
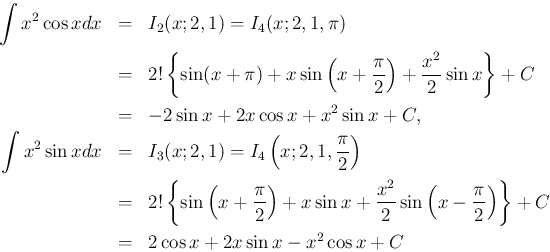
竹野茂治@新潟工科大学