2 n 次元球
まず、「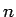 次元球」とは何であるかを述べておく。
次元球」とは何であるかを述べておく。
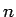 次元球とは、
次元球とは、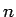 次元ユークリッド空間
次元ユークリッド空間
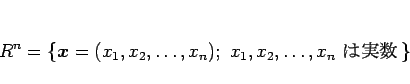
内の部分集合であり、
中心が
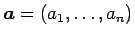 、半径
、半径 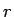
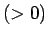 の
の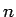 次元球
次元球
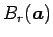 は、
は、
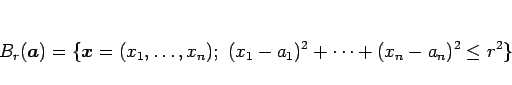 |
(1) |
と定義される。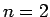 なら、
なら、
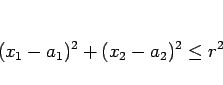
なので、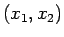 座標に対する 2 次元の円、
座標に対する 2 次元の円、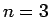 なら、
なら、
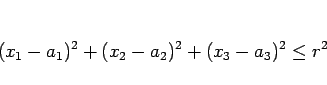
なので、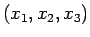 座標に対する 3 次元の球となり、
(1) はそれらの自然な
座標に対する 3 次元の球となり、
(1) はそれらの自然な 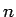 次元への拡張に
なっていることがわかるだろう。
次元への拡張に
なっていることがわかるだろう。
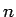 次元空間における立体の体積を測る元になるのは
次元空間における立体の体積を測る元になるのは 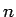 次元直方体
次元直方体
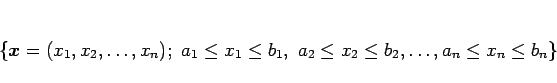 |
(2) |
の体積であり、それは、
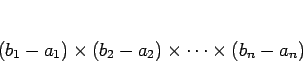 |
(3) |
と定められる。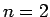 のときは、(2) は長方形、
(3) はその面積、
のときは、(2) は長方形、
(3) はその面積、
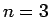 のときは、(2) は直方体、
(3) はその体積を意味していて、
よって、(2), (3) は
それらの自然な拡張になっている。
のときは、(2) は直方体、
(3) はその体積を意味していて、
よって、(2), (3) は
それらの自然な拡張になっている。
球のように曲っている図形の体積は、
大学における積分の定義と同様に、
厳密にはこの直方体を無限に埋めつくす形、
あるいは多重積分によって定義し、
その多重積分を計算するのが普通の方法なのであるが、
ここではそのあたりを多少いいかげんに考えることにする。
まず、容易に示されるように直方体は平行移動しても体積は変わらないので、
他の図形の体積もその性質を持つ。
よって、
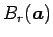 の体積は、
の体積は、
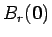 (
(
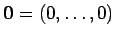 ) の体積に等しいことに注意する。
) の体積に等しいことに注意する。
また、直方体をすべての軸方向に 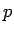 (
(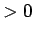 ) 倍すると、
直方体 (2) は、
) 倍すると、
直方体 (2) は、
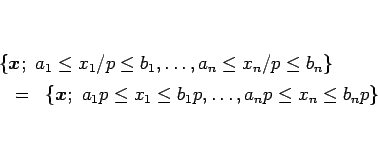
となるので、その体積は
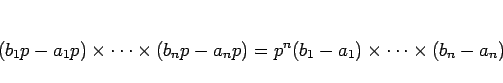
となるので、元の直方体の 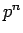 倍となり、これは他の図形でも同様である。
倍となり、これは他の図形でも同様である。
例えば、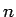 次元球の場合、
次元球の場合、
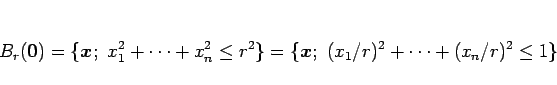
であるので、
これは半径 1 の球
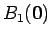 を
すべての軸方向に
を
すべての軸方向に 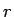 倍したものになっている。
よって、
倍したものになっている。
よって、
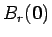 の体積 (
の体積 (
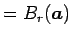 の体積) を
の体積) を
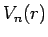 と書くことにすると、上の考察により、
と書くことにすると、上の考察により、
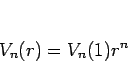
となるので、
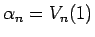 と書けば、
と書けば、
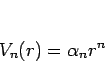 |
(4) |
となることになる。よって、この 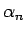 、
すなわち
、
すなわち
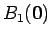 の体積を
の体積を 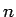 の式で表せばよい。
の式で表せばよい。
竹野茂治@新潟工科大学
2007年8月6日
![]() 次元球とは、
次元球とは、![]() 次元ユークリッド空間
次元ユークリッド空間
![]() 次元空間における立体の体積を測る元になるのは
次元空間における立体の体積を測る元になるのは ![]() 次元直方体
次元直方体
![]() の体積は、
の体積は、
![]() (
(
![]() ) の体積に等しいことに注意する。
) の体積に等しいことに注意する。
![]() (
(![]() ) 倍すると、
直方体 (2) は、
) 倍すると、
直方体 (2) は、
![]() 次元球の場合、
次元球の場合、