4 任意の列での展開

定理 3

行列式を $j$ 列目で展開すると、

$$\vert A\vert=\sum_{p=1}^n (-1)^{p+j}a_{pj}\Delta_{pj}$$ (9)

となる。また、$i$ 行目で展開すると、

$$\vert A\vert=\sum_{q=1}^n (-1)^{i+q}a_{iq}\Delta_{iq}$$ (10)

となる。

この展開公式の証明も、帰納法で得ることができる。 なお、行に関する展開公式 (10) は、 列に関する展開公式 (9) と 転置行列に対する定理 2 を組み合わせれば 容易に得られるので、ここでは (9) のみを考える。

(9) はもちろん $n=1$ の場合には明らかに成り立つので、 $(n-1)$ 次では任意の列の展開が可能だとして、 (9) を示すこととする。 なお、$j=1$ のときは行列式の定義 (1) そのものなので、 $j\geq 2$ の場合を考える。

このとき $\Delta_{pj}$ を 1 列目に関して展開すると、 $\Delta_{pj}$ の 1 列目は、$A$ の 1 列目の $p$ 行目以外の成分なので、

$$\Delta_{pj} = \sum_{k=1}^{p-1} (-1)^{k+1}a_{k1}\Delta_{pj,k1} +\sum_{k=p+1}^{n} (-1)^k a_{k1}\Delta_{pj,k1}$$ (11)

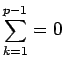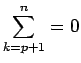となる。ただし、$p=1$ のときは $$\sum_{k=1}^{p-1}=0$$, $p=n$ のときは $$\sum_{k=p+1}^n=0$$ と考えることとする。

これを、(9) の右辺に代入すると、

$$\begin{eqnarray*} % latex2html id marker 1668 \lefteqn{\mbox{(\ref{eq:expansion}... ...p=1}^{n-1}\sum_{k=p+1}^{n} (-1)^{p+j+k}a_{pj}a_{k1}\Delta_{pj,k1}\end{eqnarray*}$$

となる。ここで、

$$\begin{eqnarray*}\sum_{p=2}^n \sum_{k=1}^{p-1} &=& \sum_{k=1}^{n-1}\sum_{p=k... ..._{k=1}^n\sum_{p=1}^{k-1} \hspace{1zw}\left(\sum_{p=1}^0=0\right)\end{eqnarray*}$$

となるので、

$${\mbox{(\ref{eq:expansion}) の右辺}}$$

$$= \sum_{k=1}^n \sum_{p=k+1}^n (-1)^{p+j+k+1}a_{pj}a_{k1}\Delta_{pj,k1} +\sum_{k=1}^n\sum_{p=1}^{k-1} (-1)^{p+j+k}a_{pj}a_{k1}\Delta_{pj,k1}$$

$$= \sum_{k=1}^n\left\{ \sum_{p=k+1}^n(-1)^{p+j+k+1}a_{pj}a_{k1}\Delta_{pj,k1} +\sum_{p=1}^{k-1} (-1)^{p+j+k}a_{pj}a_{k1}\Delta_{pj,k1} \right\}$$

$$= \sum_{k=1}^n (-1)^{k+1}a_{k1}\left\{ \sum_{p=k+1}^n(-1)^{p+j}a_{pj}\Delta_{pj,k1} +\sum_{p=1}^{k-1} (-1)^{p+j+1}a_{pj}\Delta_{pj,k1} \right\}$$ (12)

となる。

ここで、$(n-1)$ 次の行列式である $\Delta_{k1}$ は、 帰納法の仮定により $(j-1)$ 列目で展開できるが、 $\Delta_{k1}$ の $(j-1)$ 列目は $A$ の $j$ 列目の $k$ 行目以外の成分なので、よって、

$$\begin{eqnarray*}\Delta_{k1} &=& \sum_{p=1}^{k-1} (-1)^{(j-1)+p}a_{pj}\Delta_... ...pj}\Delta_{pj,k1} +\sum_{p=k+1}^n (-1)^{p+j}a_{pj}\Delta_{pj,k1}\end{eqnarray*}$$

となり、これは (12) の中括弧の中身に等しい。 よって、

$$% latex2html id marker 2210 \mbox{(\ref{eq:expansion}) の右辺} = \sum_{k=1}^n (-1)^{k+1}a_{k1}\Delta_{k1}$$

となるが、これは行列式の定義より $\vert A\vert$ に等しい。 ゆえに (9) が言えたことになる。

また、(9), (10) より、 $\vert A\vert$ は各列の成分 (または各行の成分) の 1 次式であることが言えるので、 よって、次のことも言える。

系 4

$\vert A\vert$ は各列 (または各行) に関して線形である。 すなわち、ある列が $k$ 倍されれば行列式の値は $k$ 倍となり、 ある列が 2 つの列ベクトルの和であれば、 それぞれをその列とした行列式の和になり、 さらにある列の要素がすべて 0 であれば行列式の値は 0 となる。

これにより、行列式を $n$ 個の列ベクトルの関数と見た場合、 そのそれぞれに関して線形である、ということになるので、 これを 多重線形性 と呼ぶことがある。