|
|
(9) |
を用いる方法もある。この公式も、形式的に部分積分を用いて得られる。
[f'] = s
[f] - f (0),
[f''] = s2
[f] - sf (0) - f'(0)
(9)
| = | |||
| = | 0 - f (0) - |
||
| = | s |
f'' に対しては、この公式を 2 度用いれば、
として得られる。
[f''] = s
[f'] - f'(0) = s
s
[f] - f (0)
- f'(0) = s2
[f] - sf (0) - f'(0)
今、 f (t) = t sin t とすると、
なので、
f' = (t)'sin t + t(sin t)' = sin t + t cos t
となる。これをラプラス変換すると、
f'' = (sin t)' + (t)'cos t + t(cos t)' = 2 cos t - t sin t = 2 cos t - f
となるが、上の計算より f (0) = f'(0) = 0 であり、よってこの左辺は
[f''] =
[2 cos t] -
[f]
となる。よって、
(s2 +1)[f] =
[2 cos t]
となる。
[f] =
[2 cos t] =
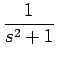
=
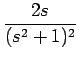
竹野茂治@新潟工科大学