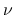
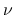 を決定する議論は, 前半部分と後半部分に分かれていて, その前半部分は,
を決定する議論は, 前半部分と後半部分に分かれていて, その前半部分は, であるが, ここは標準的な方法でよいので本稿では省略する. なお, その部分は, DiPerna[3] の漸近エントロピー対を 使用する方法よりも, Lions-Perthame-Souganidis[4] による 核エントロピー対を利用する方法の方がスマートである. 詳しくは参考文献[9] を参照.の台, すなわち
が 0 でない集合の閉包 (
) を含む, 最小の三角領域を
とすると, その台は点
を含む.
また, 本節では断わらない限り 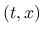 は固定して考えるので,
は固定して考えるので, 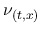 は
は 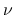 とも略記する (
とも略記する (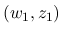 は
は 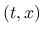 毎に
決まる値). そして
毎に
決まる値). そして 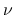 での積分において, 本節では被積分関数は,
での積分において, 本節では被積分関数は, 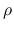 ,
, 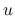 ではなく
ではなく 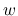 ,
, 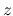 を変数とする関数と見て考える.
を変数とする関数と見て考える.
本稿では, 後半部分, すなわち 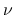 の台が
の台が 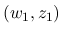 のみである, ということを示す部分についての改良を行う.
この後半部分では, 3 節で紹介した Darboux エントロピー対, 核エントロピー対から, (1) の左辺に表われる以下のような
のみである, ということを示す部分についての改良を行う.
この後半部分では, 3 節で紹介した Darboux エントロピー対, 核エントロピー対から, (1) の左辺に表われる以下のような
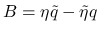 の式を主に考える.
の式を主に考える.
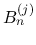 (
(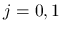 ) の
) の 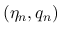 を
を
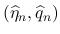 に変えたものを
に変えたものを
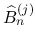 とする.
とする.
DiPerna[3], Ding-Chen-Luo[2] は, 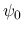 ,
,
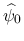 を
を 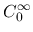 から取り, 強い制限を与えることで,
から取り, 強い制限を与えることで,
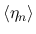 ,
,
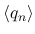 ,
,
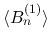 が有界で,
が有界で,
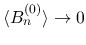 を示すことで
を示すことで
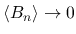 を示すのであるが, むしろ次の関係式を用いることでその議論を易しくし,
を示すのであるが, むしろ次の関係式を用いることでその議論を易しくし, 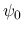 ,
,
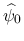 の制限を緩くすることができる.
の制限を緩くすることができる.
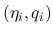 (
(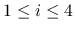 ) に対して
) に対して
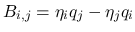 とすると,
とすると,
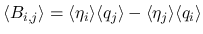
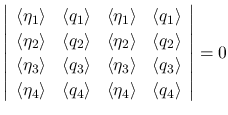
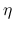 ,
, 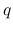 に現れない
に現れない 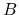 だけの
関係式 (25) を用いて, さらに
だけの
関係式 (25) を用いて, さらに 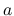 による積分を用いることで, DiPerna[3], Ding-Chen-Luo[2] の行う長い評価の議論を
簡略化する.
なお,
による積分を用いることで, DiPerna[3], Ding-Chen-Luo[2] の行う長い評価の議論を
簡略化する.
なお, 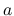 による積分の利用は, Lions-Perthame-Souganidis[4] も
用いている手法である.
による積分の利用は, Lions-Perthame-Souganidis[4] も
用いている手法である.
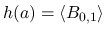 とすると,
とすると, 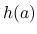 は,
は, 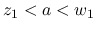 では正で, その外では 0 の連続関数.
では正で, その外では 0 の連続関数.
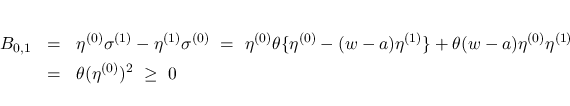
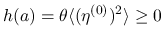 となる.
となる.
また,
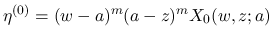 は,
は, 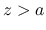 または
または 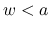 では 0 であり,
では 0 であり, 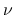 の台は
の台は
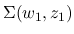 に含まれるので,
に含まれるので, 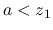 か
か 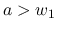 ならば
ならば 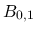 の台と
の台と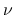 の台は
交わらないので
の台は
交わらないので
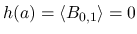 となる.
となる.
そして, 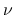 の台は点
の台は点 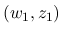 を含み,
を含み, 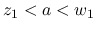 の場合は
の場合は
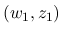 では
では 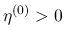 なので
なので 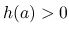 となる
こともわかる.
となる
こともわかる.
最後に 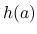 の連続性であるが,
の連続性であるが,
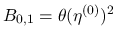 は
は 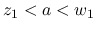 で有界で
で有界で
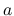 に関して連続なので, Lebesgue 収束定理により
に関して連続なので, Lebesgue 収束定理により 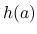 の
連続性も成り立つ.
の
連続性も成り立つ.
竹野茂治@新潟工科大学