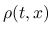 ,
, 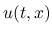 が
滑らかであれば,
が
滑らかであれば,
方程式 (3) は, 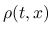 ,
, 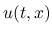 が
滑らかであれば,
が
滑らかであれば,
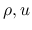 の関数の組
の関数の組
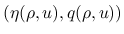 を, 「一般化エントロピー対」と呼び,
を, 「一般化エントロピー対」と呼び, 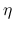 を「エントロピー」,
を「エントロピー」, 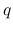 を「エントロピー流束」と呼ぶ.
エントロピー対は, 滑らかな
を「エントロピー流束」と呼ぶ.
エントロピー対は, 滑らかな
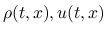 に対しては,
の追加保存則形の式を満たし, 物理的なエントロピー対
に対しては,
の追加保存則形の式を満たし, 物理的なエントロピー対
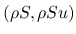 に
対応することからそう名付けられている.
また, 真空
に
対応することからそう名付けられている.
また, 真空 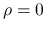 で 0 となるエントロピー (
で 0 となるエントロピー (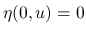 ) を
「弱エントロピー」と呼ぶ. 大きさや変動に制限のない初期値に対する
初期値問題では, 弱解に真空が現れうるため弱エントロピーを用いる必要がある.
なお, 滑らかとは限らない弱解に対しては, 一般には (6) は成立しないが, 逆に弱解の物理的な適切性の保証として, 弱解は, 凸なエントロピー
) を
「弱エントロピー」と呼ぶ. 大きさや変動に制限のない初期値に対する
初期値問題では, 弱解に真空が現れうるため弱エントロピーを用いる必要がある.
なお, 滑らかとは限らない弱解に対しては, 一般には (6) は成立しないが, 逆に弱解の物理的な適切性の保証として, 弱解は, 凸なエントロピー 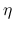 に対するエントロピー不等式
を満たす必要がある.
これは, 物理でのエントロピー増大則 (
に対するエントロピー不等式
を満たす必要がある.
これは, 物理でのエントロピー増大則 (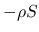 が凸) に対応する.
が凸) に対応する.
補償コンパクト性理論では, 非線形な汎弱極限を記述する, 以下の Young 測度と呼ばれるものが重要な働きをする:
,
で
は有界閉集合,
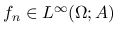
とすると, 以下を満たす
の部分列
と,
と,
のほとんど 至るところの
に対して定義される
上の確率測度 (非負で全測度 1 の Borel 測度) の族
が存在する.
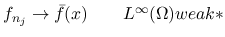
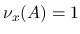
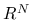 上の任意の連続関数
上の任意の連続関数 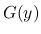 に対し,
に対し, 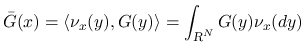
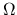 上の可測関数で,
上の可測関数で, 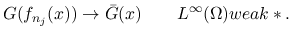
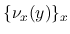 を
を 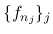 に
対する「Young 測度」と呼び,
に
対する「Young 測度」と呼び, 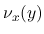 に関する
に関する 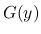 の
積分を
の
積分を
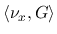 ,
,
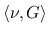 ,
,
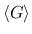 などの
ように書く.
などの
ように書く.
一様有界な関数列 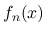 からは汎弱収束 (weak
からは汎弱収束 (weak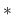 ) す
るような部分列が取れるが, 汎弱収束のような弱い収束では,
) す
るような部分列が取れるが, 汎弱収束のような弱い収束では, 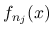 が
が 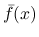 に収束しても, 一般にはそれを非線形関数
に収束しても, 一般にはそれを非線形関数 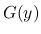 に代入した
に代入した 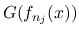 は,
は, 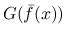 に収束するとは言えない.
例えば
に収束するとは言えない.
例えば
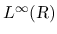 の汎弱収束では
の汎弱収束では
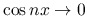 であるが,
であるが,
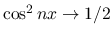 となる.
その
となる.
その 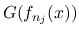 の極限を,
の極限を, 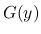 の確率測度での積分 (平均値) として記述するような測度が, Young 測度である. ちなみに,
の確率測度での積分 (平均値) として記述するような測度が, Young 測度である. ちなみに, 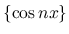 に対する Young 測度
に対する Young 測度 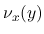 は, 非特異な絶対連続測度
は, 非特異な絶対連続測度
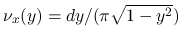 となる[10].
となる[10].
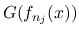 の極限が通常の
の極限が通常の 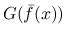 になることは, Young 測度で言えば
になることは, Young 測度で言えば 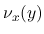 がデルタ関数
がデルタ関数
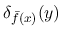 で
あることを意味し, その場合は
で
あることを意味し, その場合は 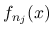 が
が 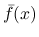 に
強収束する.
に
強収束する.
方程式 (3) に対する近似解の有界性から
得られる Young 測度
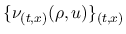 を, この方程式に豊富に存在する弱エントロピー対に対して
適用したのが Tartar 方程式 (2) に現れる各項で, さらに (3) に対して補償コンパクト性理論
を用いて得られる関係式が Tartar 方程式 (2) で
ある.
Young 測度
を, この方程式に豊富に存在する弱エントロピー対に対して
適用したのが Tartar 方程式 (2) に現れる各項で, さらに (3) に対して補償コンパクト性理論
を用いて得られる関係式が Tartar 方程式 (2) で
ある.
Young 測度
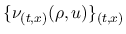 が
デルタ関数であることを決定することが, 近似解の強収束性と弱解の存在を示すことになるので, この方法では任意の弱エントロピー対に対して成立する Tartar 方程式 (2) から Young 測度を決定することが目標となる.
が
デルタ関数であることを決定することが, 近似解の強収束性と弱解の存在を示すことになるので, この方法では任意の弱エントロピー対に対して成立する Tartar 方程式 (2) から Young 測度を決定することが目標となる.
竹野茂治@新潟工科大学