9 Bn の変形
8 節により
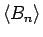 が 0 に収束することがわかったが、
この
が 0 に収束することがわかったが、
この 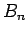 にも
にも 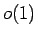 な項が含まれているので、
ここでそれらを洗い出して分離しておくことにする。
な項が含まれているので、
ここでそれらを洗い出して分離しておくことにする。
まず、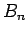 を展開して以下のように分ける。
を展開して以下のように分ける。
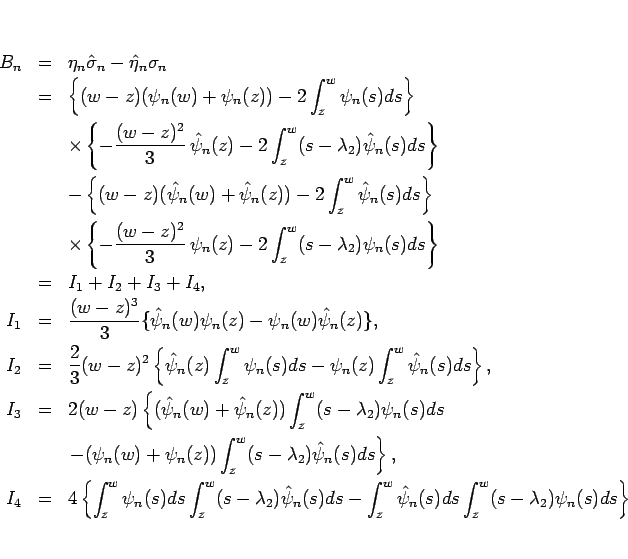
このとき 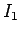 は、
は、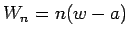 ,
, 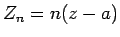 により
により
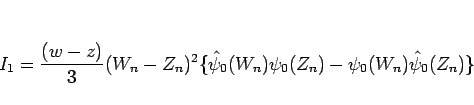
と書けるが、例えば
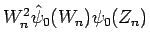 は
補題 11 の証明と同様にして、
は
補題 11 の証明と同様にして、
![$w,z,a\in[z_1,w_1]$](img522.gif) (
(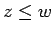 ),
), 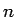 に関して有界で
かつ 0 に収束することがわかる。
これと同様にして、
に関して有界で
かつ 0 に収束することがわかる。
これと同様にして、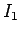 のすべての項が有界で 0 に収束することが示される。
のすべての項が有界で 0 に収束することが示される。
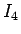 も、補題 11 により有界で、
も、補題 11 により有界で、
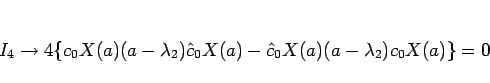
となる。
また 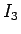 は、
は、
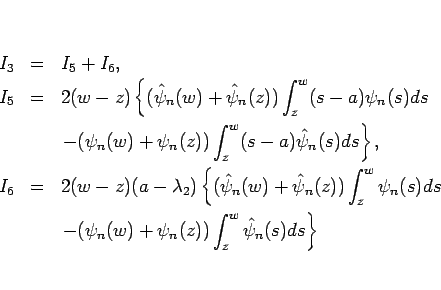
と分け、
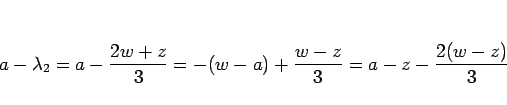
と考えると、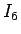 はさらに
はさらに
![\begin{eqnarray*}I_6 &=& I_7+I_8,\\
I_7
&=&
\frac{2}{3}(w-z)^2\left\{\hat{\ps...
...{-(w-a)\psi_n(w)+(a-z)\psi_n(z)\}\int_z^w\hat{\psi}_n(s)ds\right]\end{eqnarray*}](img549.gif)
と分けることができ、
補題 11 により 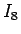 は有界で 0 に収束することがわかる。
は有界で 0 に収束することがわかる。
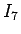 には
には 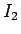 に同類項が含まれるので、それらをまとめると結局次が言える。
に同類項が含まれるので、それらをまとめると結局次が言える。
命題 13
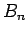 は、
は、
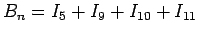 と分けることができ、
と分けることができ、
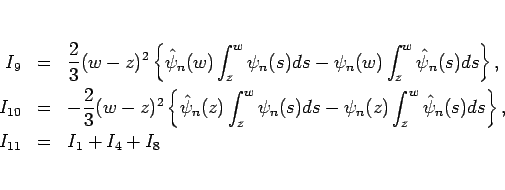
で、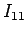 は
は
![$w,z,a\in[z_1,w_1]$](img522.gif) (
(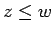 ),
), 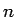 に関して有界で
かつ 0 に収束する。
に関して有界で
かつ 0 に収束する。
なお、この 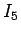 は有界ではあるが 0 には収束せず、
また
は有界ではあるが 0 には収束せず、
また 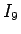 ,
, 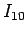 は
は 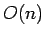 な項である。
な項である。
竹野茂治@新潟工科大学
2010年1月6日
![]() を展開して以下のように分ける。
を展開して以下のように分ける。
![]() も、補題 11 により有界で、
も、補題 11 により有界で、
![]() は、
は、
![]() は、
は、
![]() と分けることができ、
と分けることができ、
![]() は有界ではあるが 0 には収束せず、
また
は有界ではあるが 0 には収束せず、
また ![]() ,
, ![]() は
は ![]() な項である。
な項である。