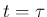
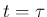 で 2 つずつの front の、複数の衝突の !(T2) の状態を
解消する。
当然、それらの衝突位置
で 2 つずつの front の、複数の衝突の !(T2) の状態を
解消する。
当然、それらの衝突位置 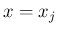 (
(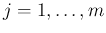 ) の間に
別の衝突のない front が挟まる場合もありうる。
今、
) の間に
別の衝突のない front が挟まる場合もありうる。
今、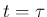 でのすべての front の位置を
でのすべての front の位置を 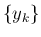 とする。
また、
とする。
また、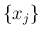 は左から順に並べた衝突位置であるとする。
は左から順に並べた衝突位置であるとする。
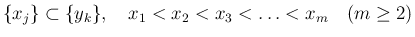
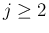 に対する各衝突点
に対する各衝突点 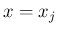 で、右の方の front の速度を
わずかに上げることで衝突時刻を少し遅らせ、
それぞれ
で、右の方の front の速度を
わずかに上げることで衝突時刻を少し遅らせ、
それぞれ
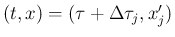 で
衝突するようにする。ここで、
で
衝突するようにする。ここで、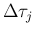 は、
となるようにする (図6)。
ここで、
は、
となるようにする (図6)。
ここで、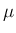 は、
は、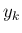 同士の間隔の最も狭い幅とし、
右の front の変更位置も、
その右隣の front との間隔は
同士の間隔の最も狭い幅とし、
右の front の変更位置も、
その右隣の front との間隔は 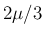 より大であるとする。
これも右、すなわち
より大であるとする。
これも右、すなわち 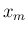 の方から順に左に行っていけばよい。
の方から順に左に行っていけばよい。
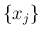 以外の front は、その速度の絶対値は
以外の front は、その速度の絶対値は 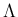 以下なので、
隣の front との間隔が
以下なので、
隣の front との間隔が 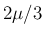 より大であれば
より大であれば
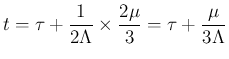
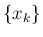 に関係する front を含め) 他の front と衝突することはない。
に関係する front を含め) 他の front と衝突することはない。
つまり、上の作業によりできる新たな
衝突点
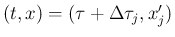 (
(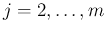 ) は、
この順で
) は、
この順で
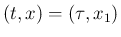 に続く衝突点で、
この間に他の front の衝突時刻が入りこんでくることはない。
に続く衝突点で、
この間に他の front の衝突時刻が入りこんでくることはない。
これで、
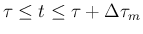 の間で他の front とも
ぶつからないように !(T2) を解消できたことになる。
そして、これらの操作では、今回速度を変更した front はすべて
の間で他の front とも
ぶつからないように !(T2) を解消できたことになる。
そして、これらの操作では、今回速度を変更した front はすべて
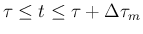 の間で他の front と衝突し、
そこから新たな、速度変更を行う前の front が発生するので、
速度変更はこの
の間で他の front と衝突し、
そこから新たな、速度変更を行う前の front が発生するので、
速度変更はこの
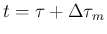 までで終わっている。
よって
までで終わっている。
よって
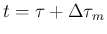 からその次の衝突までの front は
すべて速度変更を行う前の front であり、
当然 !(T4) は起こらない。
これで、
からその次の衝突までの front は
すべて速度変更を行う前の front であり、
当然 !(T4) は起こらない。
これで、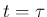 から
から
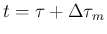 (の次の衝突時刻の手前) までは
!(T4) が起こらないように !(T2) が解消できたことになる。
(の次の衝突時刻の手前) までは
!(T4) が起こらないように !(T2) が解消できたことになる。
あとは 6.4 節、6.5 節
の操作を衝突時刻で !(T1), !(T2) が起こる度に行えばよい。
前節の解消と本節の解消を繰り返していけばよい。
その作業が高々有限で終わることは、a priori に保証されていたので、
これにより近似解がすべての 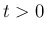 に対して大域的に作られることになる。
に対して大域的に作られることになる。
竹野茂治@新潟工科大学