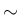
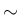 (51) の不等式を
用いて (7.75) を示すことを考える。ここも、所々詳細が省略されている。
また、ここでは
(51) の不等式を
用いて (7.75) を示すことを考える。ここも、所々詳細が省略されている。
また、ここでは 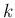 の範囲にも注意が必要である。
の範囲にも注意が必要である。
まず、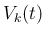 ,
, 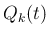 は衝突時刻以外では定数であり、よって
は衝突時刻以外では定数であり、よって
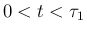 ではすべての front の世代は 1 なので、
であることに注意する。
ではすべての front の世代は 1 なので、
であることに注意する。
![\begin{eqnarray*}\Delta V_k(\tau_i)
&\leq &
\left\{\begin{array}{ll}
0 & \dis...
...ay}\right. \ &\leq &
C_0\left[\Delta Q_{k-1}(\tau_i)\right]_{-}\end{eqnarray*}](img505.png)
![$[x]_{-}=\max\{-x,0\}$](img506.png) ,
,
![$[x]_{+}=\max\{x,0\}$](img507.png) とする。
よって、(70), (71) より、
とする。
よって、(70), (71) より、
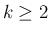 に対して、
となる。
また、(49), (50), (51)
より、
に対して、
となる。
また、(49), (50), (51)
より、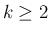 に対して、
に対して、
![\begin{eqnarray*}\Delta Q_k(\tau_i)
&\leq &
\left\{\begin{array}{ll}
-C_0\Del...
...k(\tau_i-)
+C_0\left[\Delta Q_{k-1}(\tau_i)\right]_{-}V(\tau_i-)\end{eqnarray*}](img509.png)
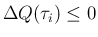 で、よって
となるので、
と書くことにすると、(70), (71), (73), (74), (75), (76) より、
で、よって
となるので、
と書くことにすると、(70), (71), (73), (74), (75), (76) より、
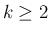 に対して
に対して
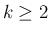 に対しては、(71) より
に対しては、(71) より
![$\displaystyle 0
\leq
Q_k(\tau_i+)
=
Q_k(\tau_1-) + \sum_{j=1}^i \Delta Q_k(\ta...
...Delta Q_k(\tau_j)\right]_{+}
-\sum_{j=1}^i \left[\Delta Q_k(\tau_j)\right]_{-}
$](img518.png)
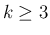 に対して
となるから、
と書けば、
に対して
となるから、
と書けば、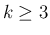 に対して
が得られることになる。
に対して
が得られることになる。
ちなみに、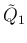 は、
は、
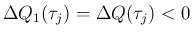 より
より
![$\displaystyle \left[\Delta Q_1(\tau_j)\right]_{+}=0$](img528.png) なので、
なので、
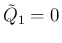 となる。
となる。
次は、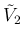 ,
, 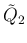 の評価を考える。
(48) より
の評価を考える。
(48) より
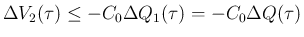
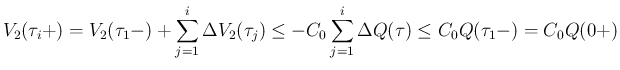
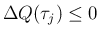 より、
となるので、
より、
となるので、
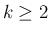 に対して、
となり、また、
(81), (87) より、
に対して、
となり、また、
(81), (87) より、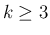 に対して、
に対して、
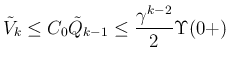
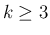 に対して、
が成り立つ。
なお、(84) より、
この (89) は
に対して、
が成り立つ。
なお、(84) より、
この (89) は 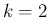 に対しても
成立することがわかる。
に対しても
成立することがわかる。
この (88), (89) が
[1] の (7.75) (p142) に対応するものであるが、
実際には少し係数や指数などが違っている。
それは、主に [1] の (7.72) (p141) と、
上の (75) の違いに起因している。
[1] は「
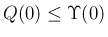 」としているが、
多分正しくは「
」としているが、
多分正しくは「
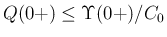 」であろう。
そのため (7.73), (7.74) の係数が少し上とは違っていて、
それでこのような違いが現れているようである。
ただし、この間違いは、この後の命題の真偽を変えるほどの
実質的なものではない。
」であろう。
そのため (7.73), (7.74) の係数が少し上とは違っていて、
それでこのような違いが現れているようである。
ただし、この間違いは、この後の命題の真偽を変えるほどの
実質的なものではない。
竹野茂治@新潟工科大学